题目内容
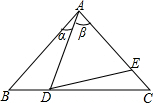 如图,△ABC中,AB=AC,点D,E分别是边BC﹑AC上的点,且AD=AE,若设∠BAD=α,∠DAC=β,则下列数量关系中正确的是( )
如图,△ABC中,AB=AC,点D,E分别是边BC﹑AC上的点,且AD=AE,若设∠BAD=α,∠DAC=β,则下列数量关系中正确的是( )| A、∠CDE=β•α | ||
B、∠CDE=
| ||
C、∠CDE=
| ||
D、∠CDE=
|
考点:等腰三角形的性质
专题:
分析:根据等腰三角形两角相等表示出∠B和∠ADE,再根据三角形的一个外角等于与它不相邻的两个内角的和列方程整理即可得解.
解答:解:∵AB=AC,
∴∠B=
(180°-α-β),
∵AD=AE,
∴∠ADE=
(180°-β),
由三角形的外角性质得,∠ADE+∠CDE=∠B+∠BAD,
所以
(180°-β)+∠CDE=
(180°-α-β)+α,
整理得∠CDE=
α.
故选C.
∴∠B=
| 1 |
| 2 |
∵AD=AE,
∴∠ADE=
| 1 |
| 2 |
由三角形的外角性质得,∠ADE+∠CDE=∠B+∠BAD,
所以
| 1 |
| 2 |
| 1 |
| 2 |
整理得∠CDE=
| 1 |
| 2 |
故选C.
点评:本题考查了等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并利用三角形的外角性质列出方程是解题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
下列叙述正确的是( )
| A、“13位同学中有两人出生的月份相同”是随机事件 |
| B、小亮掷硬币100次,其中44次正面朝上,则小亮掷硬币一次正面朝上的概率为0.44 |
| C、“明天降雨的概率是80%”,即明天下雨有80%的可能性 |
| D、彩票的中奖概率为1%,买100张才会中奖 |
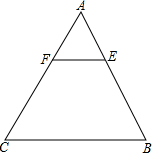 如图,在△ABC中,AE:EB=1;2,EF∥BC,求S△AEF:S△ABC的值.
如图,在△ABC中,AE:EB=1;2,EF∥BC,求S△AEF:S△ABC的值.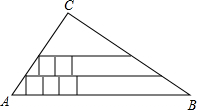 如图,在Rt△ABC中,∠C为直角,AC=6,BC=8.在Rt△ABC内从左往右叠放边长为1.2的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放
如图,在Rt△ABC中,∠C为直角,AC=6,BC=8.在Rt△ABC内从左往右叠放边长为1.2的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放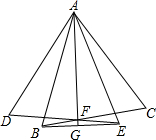 如图,等边△ABC绕点A顺时针旋转到△ADE,BC与DE相交于点F,连接AF并延长,交BE于点G,求证:AF⊥BE.
如图,等边△ABC绕点A顺时针旋转到△ADE,BC与DE相交于点F,连接AF并延长,交BE于点G,求证:AF⊥BE.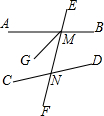 如图,图中同位角一共
如图,图中同位角一共