题目内容
 如图,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连接AE,CE,延长CE到F,使得BF=BC,连接BF,则∠F的度数等于
如图,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连接AE,CE,延长CE到F,使得BF=BC,连接BF,则∠F的度数等于考点:正方形的性质,全等三角形的判定与性质,等腰三角形的性质
专题:
分析:根据正方形的四条边都相等可得AB=BC,对角线平分一组对角可得∠ABE=∠CBE,然后利用“边角边”证明△ABE和△CBE全等,根据全等三角形对应角相等可得∠BCE=∠BAE,再根据等边对等角解答即可.
解答:解:在正方形ABCD中,AB=BC,∠ABE=∠CBE,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴∠BCE=∠BAE=15°,
∵BF=BC,
∴∠F=∠BCE=15°.
故答案为:15.
在△ABE和△CBE中,
|
∴△ABE≌△CBE(SAS),
∴∠BCE=∠BAE=15°,
∵BF=BC,
∴∠F=∠BCE=15°.
故答案为:15.
点评:本题考查了正方形的性质,全等三角形的判定与性质,等腰三角形的性质,熟记性质并确定出△ABE和△CBE全等是解题的关键,也是本题的难点.

练习册系列答案
相关题目
中国的领水面积约为370000km2,用科学记数法表示是( )
| A、3.7×103km2 |
| B、3.7×104km2 |
| C、3.7×105km2 |
| D、3.7×106km2 |
 如图所示,在数轴上有三个点A,B,C,
如图所示,在数轴上有三个点A,B,C,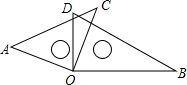 如图,将一副30°和45°的直角三角板的两个直角叠放在一起,使直角顶点重合于点O,若∠AOD=70°,则∠BOC=
如图,将一副30°和45°的直角三角板的两个直角叠放在一起,使直角顶点重合于点O,若∠AOD=70°,则∠BOC=