题目内容
【题目】如图1，在矩形ABCD中，AB=5，BC=4，E是BC边上一点，连接DE，将矩形ABCD沿DE折叠，顶点C恰好落在AB边上点F处，延长DE交AB的延长线于点G．
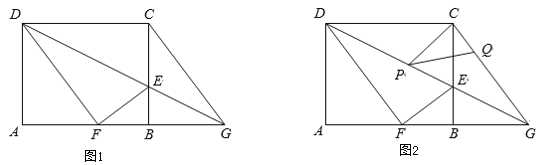
（1）求线段BE的长；
（2）连接CG，求证：四边形CDFG是菱形；
（3）如图2，P，Q分别是线段DG，CG上的动点（与端点不重合），且∠CPQ=∠CDP，是否存在这样的点P，使△CPQ是等腰三角形？若存在，请直接写出DP的值，若不存在，请说明理由．
【答案】（1）
；（2）见解析；（3）存在，
或
【解析】
（1）设
，由矩形的性质，折叠的性质和勾股定理得出BF,EF的值，然后在
中利用勾股定理即可求解；
（2）由矩形的性质得出
，然后根据平行线分线段成比例可求出BG的长度，进而可求出FG的长度，则可证明结论；
（3）分两种情况：
和
，分别利用等腰三角形的性质和相似三角形的判定及性质得出PG的长度，然后利用勾股定理求出DG的长度，最后利用
即可求解．
（1）∵四边形ABCD是矩形，
∴
．
由折叠的性质可知，
，
，
，
．
设，则
，
，
，
解得
，
；
（2）证明：
，
．
，
，
，
，
，
．
，
∴四边形CDFG是平行四边形．
∵
，
∴四边形CDFG是菱形；
（3）存在，理由如下：
①若，
∵四边形CDFG是菱形，
∴
，
．
，
．
，
，
．
，
．
，
，
；
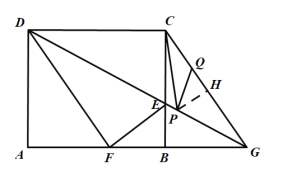
②若，
过点P作
交CG于点H，
，
．
，
，
．
，
．
∵四边形CDFG是菱形，
∴
．
，
，
，
，
，
，
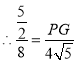综上所述，DP的值为或．
练习册系列答案
相关题目
