题目内容
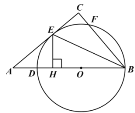
【题目】如图,在平行四边形ABCD中,AB=10,BC=15,tan∠A=![]() 点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
【答案】![]() 或
或![]() 或
或![]()
【解析】
分三种情况:点Q在直线AD上,点Q在直线CD上和点Q在直线BC上,分别求出PB的长度,然后利用扇形的面积公式即可求解.
①当点Q在直线AD上时,此时![]() ,如图,
,如图,
![]() ,
,
![]() .
.
∵![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
∴PB旋转到PQ所扫过的面积为![]() ;
;
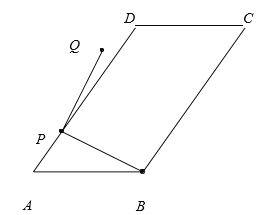
②当点Q在直线CD上时,此时![]() ,如图,
,如图,
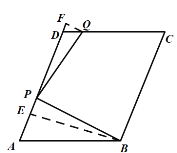
过点B作![]() 交AD于点E,过点Q作
交AD于点E,过点Q作![]() 交AD的延长线于点F,
交AD的延长线于点F,
∵四边形ABCD是平行四边形,
∴![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,
![]() .
.
由①知,![]() ,
,
设![]() ,
,
则![]() .
.
![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,
![]() ,
,
∴PB旋转到PQ所扫过的面积为![]() ;
;
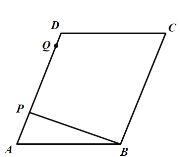
③当点Q在直线BC上时,此时![]() ,如图,
,如图,
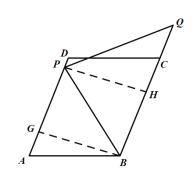
过点B作![]() 交AD于点E,过点P作
交AD于点E,过点P作![]() 交BC于点H,
交BC于点H,
∵四边形ABCD是平行四边形,
∴![]() .
.
∵![]() ,
,![]() ,
,
![]() ,
,
∴四边形BGPH是平行四边形.
∵![]() ,
,
∴四边形BGPH是矩形,
∴![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
∴PB旋转到PQ所扫过的面积为![]() ;
;
故答案为:![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目