Question

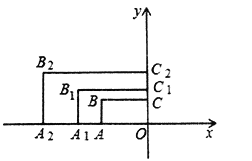
【题目】如图，在平面直角坐标系中，矩形AOCB的两边OA、OC分别在x轴和y轴上，且OA＝2，OC＝1．在第二象限内，将矩形AOCB以原点O为位似中心放大为原来的倍，得到矩形A1OC1B1，再将矩形A1OC1B1以原点O为位似中心放大倍，得到矩形A2OC2B2，以此类推，得到的矩形A2020OC2020B2020的对角线交点的纵坐标为______________．

Answer 1

【答案】；

【解析】

根据平面直角坐标系中，以原点为位似中心的位似图形的对应点坐标之间的关系，即可求解．

∵在第二象限内，将矩形AOCB以原点O为位似中心放大为原来的倍，

∴矩形A1OC1B1与矩形AOCB是位似图形，点B与点B1是对应点，

∵OA=2， OC=1，点B的坐标为（–2，1），

∴点B1的坐标为（2×，1×），

∵将矩形A1OC1B1以原点O为位似中心放大倍，得到矩形A2OC2B2，

∴B2（2××，1××），

∴Bn（2×，1×），

∴矩形AnOCnBnA的对角线交点的坐标为（2××，1××），

∴矩形A2020OC2020B2020的对角线交点的纵坐标为，

故答案为：．