题目内容
5.在△ABC中,AB=AC,AD⊥BC于点D,△ABC的周长为32cm,△ABD的周长为24cm,则AD的长为( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
分析 由已知条件根据等腰三角形三线合一的性质可得到BD=DC,再根据三角形的周长定义求解.
解答 解:∵AB=AC,AD⊥BC,
∴BD=DC.
∵AB+AC+BC=32,
即AB+BD+CD+AC=32,
∴AC+DC=16
∴AC+DC+AD=24
∴AD=8cm.
故选B.
点评 本题考查等腰三角形的性质;由已知条件结合图形发现并利用AC+CD是△ABC的周长的一半是正确解答本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
10.5a+( )=5a-2a2-b.
| A. | 2a2+b | B. | 2a2-b | C. | -2a2+b | D. | -2a2-b |
14.填表:
| 单项式 | -$\frac{{a}^{2}{b}^{3}c}{2}$ | -0.5xyz2 | m | 0 | 3a2b |
| 系数 | -$\frac{1}{2}$ | -0.5 | 1 | 0 | 3 |
| 次数 | 6 | 4 | 1 | 0 | 3 |
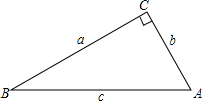 如图,在Rt△ABC中,∠C=90°.
如图,在Rt△ABC中,∠C=90°.