题目内容
12.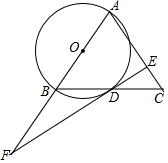 如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作⊙O的切线DE交AC于点E,交AB延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作⊙O的切线DE交AC于点E,交AB延长线于点F.(1)求证:DE⊥AC;
(2)若AB=10,AE=8,求BF的长.
分析 (1)连接OD、AD,由AB=AC且∠ADB=90°知D是BC的中点,由O是AB中点知OD∥AC,根据OD⊥DE可得;
(2)证△ODF∽△AEF得$\frac{OD}{AE}$=$\frac{OF}{AF}$,据此可得答案.
解答 解:(1)连接OD、AD,
∵DE切⊙O于点D,
∴OD⊥DE,
∵AB是直径,
∴∠ADB=90°,
∵AB=AC,
∴D是BC的中点,
又∵O是AB中点,
∴OD∥AC,
∴DE⊥AC;
(2)∵AB=10,
∴OB=OD=5,
由(1)得OD∥AC,
∴△ODF∽△AEF,
∴$\frac{OD}{AE}$=$\frac{OF}{AF}$=$\frac{BF+OB}{BF+AB}$,
设BF=x,AE=8,
∴$\frac{5}{8}$=$\frac{x+5}{x+10}$,
解得:x=$\frac{10}{3}$,
经检验x=$\frac{10}{3}$是原分式方程的根,且符合题意,
∴BF=$\frac{10}{3}$.
点评 本题主要考查等腰三角形的性质、切线的性质及相似三角形的判定与性质,熟练掌握等腰三角形的性质、切线的性质及相似三角形的判定与性质是解题的关键.

练习册系列答案
相关题目
20.下列计算正确的是( )
| A. | 3m-m=2 | B. | m4÷m3=m | C. | (-m2)3=m6 | D. | -(m-n)=m+n |
17.关于一组数据:1,5,6,3,5,下列说法错误的是( )
| A. | 平均数是4 | B. | 众数是5 | C. | 中位数是6 | D. | 方差是3.2 |

 解不等式组$\left\{\begin{array}{l}{5x+1>3(x-1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$,并把它的解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{5x+1>3(x-1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$,并把它的解集在数轴上表示出来.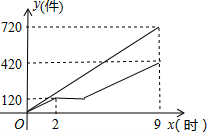 甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.
甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.