题目内容
18. 如图,把等腰直角三角尺的直角顶点放在直尺的一边上,则∠1+∠2=135°.
如图,把等腰直角三角尺的直角顶点放在直尺的一边上,则∠1+∠2=135°.
分析 根据等腰直角三角形得出∠ACB=90°,∠A=∠B=45°,根据平行线性质求出∠1=∠ACM,根据三角形外角性质求出∠2=∠B+∠BCM,求出∠1+∠2=∠ACB+∠B即可.
解答 解:如图:
∵△ACB是等腰直角三角形,
∴∠ACB=90°,∠A=∠B=45°,
∵EF∥MN,
∴∠1=∠ACM,
∵∠2=∠B+∠BCM,
∴∠1+∠2=∠ACM+∠B+∠BCM
=∠ACB+∠B
=90°+45°
=135°,
故答案为:135°.
点评 本题考查了平行线的性质,等腰直角三角形,三角形的外角性质的应用,能求出∠1+∠2=∠ACB+∠B是解此题的关键,题目比较典型,难度适中.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
8.一个三角形所有的中线、高和角平分线的条数为7,则此三角形的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
9. 如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于点A(2,6),B(n,-3)两点.请根据图象写出一次函数值大于反比例函数值时x的取值范围-4<x<0或x>2.
如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于点A(2,6),B(n,-3)两点.请根据图象写出一次函数值大于反比例函数值时x的取值范围-4<x<0或x>2.
 如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于点A(2,6),B(n,-3)两点.请根据图象写出一次函数值大于反比例函数值时x的取值范围-4<x<0或x>2.
如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于点A(2,6),B(n,-3)两点.请根据图象写出一次函数值大于反比例函数值时x的取值范围-4<x<0或x>2.
10.给出五种图形:①矩形,②菱形,③等腰三角形(腰与底边不相等),④等边三角形,⑤平行四边形(不含矩形,菱形).其中可用两块能完全重合的含有30°角的三角板拼成的所有图形是( )
| A. | ①、②、③ | B. | ②、④、⑤ | C. | ①、③、④、⑤ | D. | ①、②、③、④、⑤ |
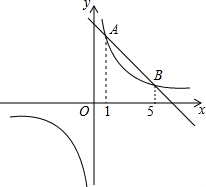 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,它们的横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}-b$的解集是0<x<1或x>5.
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,它们的横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}-b$的解集是0<x<1或x>5.