题目内容
6．
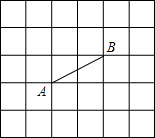如图，线段AB是一条格点线段．（1）画一条线段，使它与线段AB有一个公共端点．且与线段AB相等．并证明这两条线段相等；
（2）在所给的网格中．你最多能画出几条满足（1）中要求的线段？
分析 （1）找到直角边为1和2的直角三角形的斜边，根据勾股定理即可求解；
（2）找到直角边为1和2的所有直角三角形的斜边即可．
解答 解：（1）由勾股定理可得AB=AC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，
故这两条线段相等；
（2）如图所示：
故在所给的网格中．最多能画出14条满足（1）中要求的线段．
点评 考查了勾股定理，勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
已知有理数a在数轴上的位置如图所示，把a，a的相反数，a的倒数，a的绝对值，a的负倒数按从小到大的顺序用“＜”连接起来．
如图，△ABC的高AD，BE相交于点F．
5．
已知有理数a、b在数轴上表示的点如图所示，则下列式子中正确的是（ ）
已知有理数a、b在数轴上表示的点如图所示，则下列式子中正确的是（ ）| A． | a+b＞0 | B． | a-b＜0 | C． | ab＞0 | D． | $\frac{a}{b}＜0$ |
6．
如图，Rt△ABC中，∠ACB=90°，∠B=30°，AC=2，将△ABC绕点C逆时针旋转至△A′B′C，使得点A′恰好落在AB上，A′B′与BC交于点D，则△A′CD的面积为（ ）
如图，Rt△ABC中，∠ACB=90°，∠B=30°，AC=2，将△ABC绕点C逆时针旋转至△A′B′C，使得点A′恰好落在AB上，A′B′与BC交于点D，则△A′CD的面积为（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | 3$\sqrt{3}$ | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |