题目内容
5.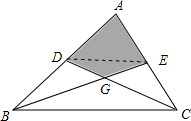 如图,在△ABC中,中线CD,BE交于点G,已知△ABC的面积等于4,求四边形ADGE的面积.
如图,在△ABC中,中线CD,BE交于点G,已知△ABC的面积等于4,求四边形ADGE的面积.
分析 根据三角形中位线定理得到DE∥BC,DE=$\frac{1}{2}$BC,得到△ADE∽△ABC,且相似比是$\frac{1}{2}$,根据相似三角形的性质求出S△ADE的面积,根据重心的概念求出S△EDG的面积,计算即可.
解答 解:∵CD,BE是△ABC的中线,
∴G是△ABC的重心,DE∥BC,DE=$\frac{1}{2}$BC,
∴△ADE∽△ABC,又DE=$\frac{1}{2}$BC,
∴S△ADE=1,
∴S△EDC=1,又DG=$\frac{1}{2}$GC,
∴S△EDG=$\frac{1}{3}$,
∴四边形ADGE的面积=S△ADE+S△EDG=$\frac{4}{3}$.
点评 本题考查的是三角形的重心、相似三角形的性质、三角形的中位线定理,掌握三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键.

练习册系列答案
相关题目
14.将抛物线y=5x2向右平移1个单位长后,所得到的函数解析式为( )
| A. | y=5x2+1 | B. | y=5x2-1 | C. | y=5(x-1)2 | D. | y=5(x+1)2 |
15. 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )
 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )| A. | 点P在线段AB的延长线上 | B. | 点P在线段BA的延长线上 | ||
| C. | 点P在射线AB的延长线上 | D. | 点P在直线AB的延长线上 |
 如图,在△ABC中,AB=AD=CD,∠CAD-∠BAD=10°,求∠B和∠C的度数.
如图,在△ABC中,AB=AD=CD,∠CAD-∠BAD=10°,求∠B和∠C的度数.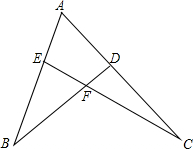 已知,如图,点D、E分别在AC、AB上,BD、CE交于F,∠B:∠C=3:2.
已知,如图,点D、E分别在AC、AB上,BD、CE交于F,∠B:∠C=3:2.