题目内容
9.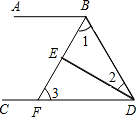 如图,∠ABD和∠BDC的平分线交于点E,BE交CD于点F,∠1+∠2=90°.
如图,∠ABD和∠BDC的平分线交于点E,BE交CD于点F,∠1+∠2=90°.求证:(1)AB∥CD;
(2)∠2+∠3=90°.
分析 (1)根据角平分线得:∠ABD=2∠1,∠CDB=2∠2,由∠1+∠2=90°得:∠ABD+∠CDB=180°,则AB∥CD;
(2)由平行线的性质得:∠3=∠ABF,由角平分线定义得∠1=∠ABF,则∠1=∠3,再由三角形内角和可得结论.
解答 证明:(1)∵∠ABD和∠BDC的平分线交于点E,
∴∠ABD=2∠1,∠CDB=2∠2,
∵∠1+∠2=90°
∴∠ABD+∠CDB=2∠1+2∠2=180°,
∴AB∥CD;
(2)∵AB∥CD,
∴∠3=∠ABF,
∵∠1=∠ABF,
∴∠1=∠3,
∵∠2=∠FDE,∠1+∠3+∠2+∠FDE=180°,
∴2∠3+2∠2=180°,
∴∠3+∠2=90°.
点评 本题考查了平行线的判定、角平分线的定义、三角形内角和定理,属于基础题,能综合运用定理进行推理是解此题的关键,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 点A,B,C的位置如图所示,按下列要求画出图形并回答问题.
点A,B,C的位置如图所示,按下列要求画出图形并回答问题. 如图,把直角三角形的直角顶点放在两条平行线a,b上,已知∠1=40°,则∠2=50°.
如图,把直角三角形的直角顶点放在两条平行线a,b上,已知∠1=40°,则∠2=50°.