题目内容
如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2,垂足为D,过点O,B的直线l4交l2于点E,当直线l1,l2,l3能围成三角形时,设该三角形面积为S1,当直线l2,l3,l4能围成三角形时,设该三角形面积为S2.(1)若点B在线段AC上,且S1=S2,则B点坐标为 ;
(2)若点B在直线l1上,且S2=
 S1,则∠BOA的度数为 .
S1,则∠BOA的度数为 .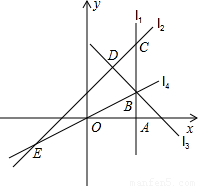
【答案】分析:(1)设B的坐标是(2,m),则△BCD是等腰直角三角形,即可表示出S1,求得直线l1的解析式,解方程组即可求得E的坐标,则S2的值即可求得,根据S1=S2,即可得到一个关于m的方程从而求得m的值;
(2)根据S2=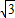 S1,即可得到一个关于m的方程从而求得m的值,得到AB的长,从而求得∠BOA的正切值,求得角的度数.
S1,即可得到一个关于m的方程从而求得m的值,得到AB的长,从而求得∠BOA的正切值,求得角的度数.
解答:解:(1)设B的坐标是(2,m),则△BCD是等腰直角三角形.
BC=|3-m|,
则BD=CD=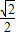 BC=
BC=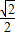 |3-m|,S1=
|3-m|,S1= ×(
×(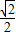 |3-m|)2=
|3-m|)2= (3-m)2.
(3-m)2.
设直线l4的解析式是y=kx,则2k=m,解得:k=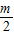 ,
,
则直线的解析式是y=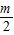 x.
x.
根据题意得: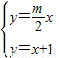 ,解得:
,解得: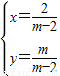 ,
,
则E的坐标是(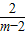 ,
,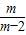 ).
).
S△BCE= BC•|
BC•|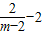 |=
|= |3-m|•|
|3-m|•|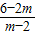 |=
|=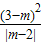 .
.
∴S2=S△BCE-S1=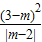 -
- (3-m)2.
(3-m)2.
当S1=S2时,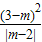 -
- (3-m)2=
(3-m)2= (3-m)2.
(3-m)2.
解得:m1=4(不合题意舍去)或m2=0,
则B的坐标是(2,0);
(2)当S2=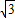 S1时,
S1时,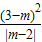 -
- (3-m)2=
(3-m)2=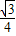 (3-m)2.
(3-m)2.
解得:m=4+2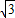 或4-2
或4-2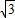 .
.
则AB=4+2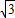 或4-2
或4-2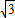 .
.
∴tan∠BOA=2+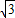 或2-
或2-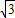 .
.
∴∠BOA=75°或15°.
点评:本题考查了一次函数与三角函数,三角形的面积,正确表示出S2是关键.
(2)根据S2=
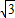 S1,即可得到一个关于m的方程从而求得m的值,得到AB的长,从而求得∠BOA的正切值,求得角的度数.
S1,即可得到一个关于m的方程从而求得m的值,得到AB的长,从而求得∠BOA的正切值,求得角的度数.解答:解:(1)设B的坐标是(2,m),则△BCD是等腰直角三角形.
BC=|3-m|,
则BD=CD=
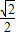 BC=
BC=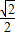 |3-m|,S1=
|3-m|,S1= ×(
×(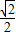 |3-m|)2=
|3-m|)2= (3-m)2.
(3-m)2.设直线l4的解析式是y=kx,则2k=m,解得:k=
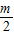 ,
,则直线的解析式是y=
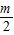 x.
x.根据题意得:
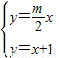 ,解得:
,解得: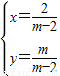 ,
,则E的坐标是(
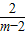 ,
,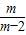 ).
).S△BCE=
 BC•|
BC•|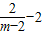 |=
|= |3-m|•|
|3-m|•|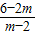 |=
|=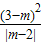 .
.∴S2=S△BCE-S1=
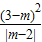 -
- (3-m)2.
(3-m)2.当S1=S2时,
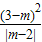 -
- (3-m)2=
(3-m)2= (3-m)2.
(3-m)2.解得:m1=4(不合题意舍去)或m2=0,
则B的坐标是(2,0);
(2)当S2=
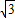 S1时,
S1时,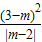 -
- (3-m)2=
(3-m)2=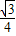 (3-m)2.
(3-m)2.解得:m=4+2
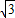 或4-2
或4-2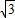 .
.则AB=4+2
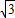 或4-2
或4-2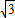 .
.∴tan∠BOA=2+
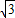 或2-
或2-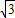 .
.∴∠BOA=75°或15°.
点评:本题考查了一次函数与三角函数,三角形的面积,正确表示出S2是关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 (2012•宁波模拟)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…,直线ln⊥x轴于点(n,0)(n为正整数).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=2x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn.如果△OA1B1的面积记作S,四边形A1A2B2B1的面积记作S1,四边形A2A3B3B2的面积记作S2,…,四边形AnAn+1Bn+1Bn的面积记作Sn,那么S1=
(2012•宁波模拟)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…,直线ln⊥x轴于点(n,0)(n为正整数).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=2x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn.如果△OA1B1的面积记作S,四边形A1A2B2B1的面积记作S1,四边形A2A3B3B2的面积记作S2,…,四边形AnAn+1Bn+1Bn的面积记作Sn,那么S1= (2012•张家口一模)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…ln分别交于点A1,A2,A3,…An;函数y=2x的图象与直线l1,l2,l3,…ln分别交于点B1,B2,B3,…Bn.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…四边形An-1AnBnBn-1的面积记作Sn,那么S2012=
(2012•张家口一模)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…ln分别交于点A1,A2,A3,…An;函数y=2x的图象与直线l1,l2,l3,…ln分别交于点B1,B2,B3,…Bn.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…四边形An-1AnBnBn-1的面积记作Sn,那么S2012= (2013•义乌市)如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2,垂足为D,过点O,B的直线l4交l2于点E,当直线l1,l2,l3能围成三角形时,设该三角形面积为S1,当直线l2,l3,l4能围成三角形时,设该三角形面积为S2.
(2013•义乌市)如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2,垂足为D,过点O,B的直线l4交l2于点E,当直线l1,l2,l3能围成三角形时,设该三角形面积为S1,当直线l2,l3,l4能围成三角形时,设该三角形面积为S2.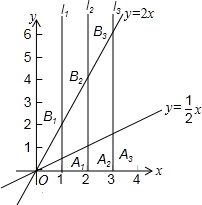 如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=
如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=