题目内容
 (2012•张家口一模)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…ln分别交于点A1,A2,A3,…An;函数y=2x的图象与直线l1,l2,l3,…ln分别交于点B1,B2,B3,…Bn.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…四边形An-1AnBnBn-1的面积记作Sn,那么S2012=
(2012•张家口一模)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…ln分别交于点A1,A2,A3,…An;函数y=2x的图象与直线l1,l2,l3,…ln分别交于点B1,B2,B3,…Bn.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…四边形An-1AnBnBn-1的面积记作Sn,那么S2012=2011.5
2011.5
.分析:先求出A1,A2,A3,…An和点B1,B2,B3,…Bn的坐标,利用三角形的面积公式计算△OA1B1的面积;四边形A1A2B2B1的面积,四边形A2A3B3B2的面积,…四边形An-1AnBnBn-1的面积,则通过两个三角形的面积差计算,这样得到Sn=n-
,然后把n=2012代入即可求得答案.
| 1 |
| 2 |
解答:解:∵函数y=x的图象与直线l1,l2,l3,…ln分别交于点A1,A2,A3,…An,
∴A1(1,1),A2(2,2),A3(3,3)…An(n,n),
又∵函数y=2x的图象与直线l1,l2,l3,…ln分别交于点B1,B2,B3,…Bn,
∴B1(1,2),B2(2,4),B3(3,6),…Bn(n,2n),
∴S1=
•1•(2-1),
S2=
•2•(4-2)-
•1•(2-1),
S3=
•3•(6-3)-
•2•(4-2),
…
Sn=
•n•(2n-n)-
•(n-1)[2(n-1)-(n-1)]=
n2-
(n-1)2=n-
.
当n=2012,S2012=2012-
=2011.5.
故答案为:2011.5.
∴A1(1,1),A2(2,2),A3(3,3)…An(n,n),
又∵函数y=2x的图象与直线l1,l2,l3,…ln分别交于点B1,B2,B3,…Bn,
∴B1(1,2),B2(2,4),B3(3,6),…Bn(n,2n),
∴S1=
| 1 |
| 2 |
S2=
| 1 |
| 2 |
| 1 |
| 2 |
S3=
| 1 |
| 2 |
| 1 |
| 2 |
…
Sn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当n=2012,S2012=2012-
| 1 |
| 2 |
故答案为:2011.5.
点评:此题考查了一次函数的性质、三角形的面积以及整数的混合运算等知识.此题难度较大,属于规律性题目,注意数形结合思想的应用,注意得到规律:Sn=n-
是解此题的关键.
| 1 |
| 2 |

练习册系列答案
相关题目
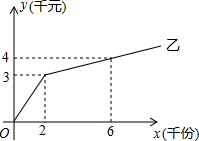 (2012•张家口一模)某单位准备印制一批书面材料,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲厂的印刷费用y(千元)与书面材料数量x(千份)的关系见下表:
(2012•张家口一模)某单位准备印制一批书面材料,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲厂的印刷费用y(千元)与书面材料数量x(千份)的关系见下表: (1)求抽取的学生人数,并根据抽查到的学生五个等级人数的分布情况,补全扇形统计图和频数分布直方图;
(1)求抽取的学生人数,并根据抽查到的学生五个等级人数的分布情况,补全扇形统计图和频数分布直方图;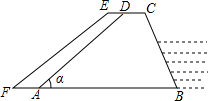 (2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米.
(2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米.