题目内容
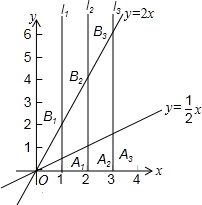 如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=
如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=| 1 |
| 2 |
分析:先求出A1,A2,A3,…An和点B1,B2,B3,…Bn的坐标,利用三角形的面积公式计算△OA1B1的面积;四边形A1A2B2B1的面积,四边形A2A3B3B2的面积,…四边形An-1AnBnBn-1的面积,则通过两个三角形的面积差计算,这样得到Sn=
n-
n,然后把n=2012代入即可求得答案.
| 3 |
| 2 |
| 3 |
| 4 |
解答:解:∵函数y=
x的图象与直线l1,l2,l3,…ln分别交于点A1,A2,A3,…An,
∴A1(1,
),A2(2,1),A3(3,
)…An(n,
n),
又∵函数y=2x的图象与直线l1,l2,l3,…ln分别交于点B1,B2,B3,…Bn,
∴B1(1,2),B2(2,4),B3(3,6),…Bn(n,2n),
∴S1=
•1•(2-
),
S2=
•2•(4-1)-
•1•(2-
),
S3=
•3•(6-
)-
•2•(4-1),
…
Sn=
•n•(2n-
n)-
•(n-1)[2(n-1)-
(n-1)]=
n-
.
当n=2012,S2012=2012×
-
=3017.25.
故选C
| 1 |
| 2 |
∴A1(1,
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
又∵函数y=2x的图象与直线l1,l2,l3,…ln分别交于点B1,B2,B3,…Bn,
∴B1(1,2),B2(2,4),B3(3,6),…Bn(n,2n),
∴S1=
| 1 |
| 2 |
| 1 |
| 2 |
S2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
S3=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
…
Sn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
当n=2012,S2012=2012×
| 3 |
| 2 |
| 3 |
| 4 |
故选C
点评:此题考查了一次函数的性质、三角形的面积以及整数的混合运算等知识.此题难度较大,属于规律性题目,注意数形结合思想的应用,注意得到规律:Sn=
n-
n是解此题的关键.
| 3 |
| 2 |
| 3 |
| 4 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•宁波模拟)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…,直线ln⊥x轴于点(n,0)(n为正整数).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=2x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn.如果△OA1B1的面积记作S,四边形A1A2B2B1的面积记作S1,四边形A2A3B3B2的面积记作S2,…,四边形AnAn+1Bn+1Bn的面积记作Sn,那么S1=
(2012•宁波模拟)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…,直线ln⊥x轴于点(n,0)(n为正整数).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=2x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn.如果△OA1B1的面积记作S,四边形A1A2B2B1的面积记作S1,四边形A2A3B3B2的面积记作S2,…,四边形AnAn+1Bn+1Bn的面积记作Sn,那么S1= (2012•张家口一模)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…ln分别交于点A1,A2,A3,…An;函数y=2x的图象与直线l1,l2,l3,…ln分别交于点B1,B2,B3,…Bn.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…四边形An-1AnBnBn-1的面积记作Sn,那么S2012=
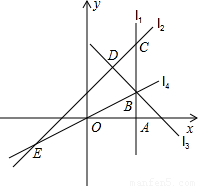
(2012•张家口一模)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…ln分别交于点A1,A2,A3,…An;函数y=2x的图象与直线l1,l2,l3,…ln分别交于点B1,B2,B3,…Bn.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…四边形An-1AnBnBn-1的面积记作Sn,那么S2012= (2013•义乌市)如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2,垂足为D,过点O,B的直线l4交l2于点E,当直线l1,l2,l3能围成三角形时,设该三角形面积为S1,当直线l2,l3,l4能围成三角形时,设该三角形面积为S2.
(2013•义乌市)如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2,垂足为D,过点O,B的直线l4交l2于点E,当直线l1,l2,l3能围成三角形时,设该三角形面积为S1,当直线l2,l3,l4能围成三角形时,设该三角形面积为S2. S1,则∠BOA的度数为 .
S1,则∠BOA的度数为 .