题目内容
 如图,∠1=∠2=30°,∠3=∠4,∠A=80°,则∠CDE=
如图,∠1=∠2=30°,∠3=∠4,∠A=80°,则∠CDE=考点:三角形内角和定理
专题:
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠CDE,再根据三角形的内角和定理求出∠3,然后利用三角形的内角和定理列式计算即可求出∠BEC.
解答:解:∵∠1=30°,∠A=80°,
∴∠CDE=∠1+∠A=30°+80°=110°,
在△BCD中,∠3+∠4=180°-∠2-∠CDE=180°-30°-110°=40°,
∵∠3=∠4,
∴∠3=
×40°=20°,
在△BCE中,∠BEC=180°-∠2-∠3=180°-30°-20°=130°.
故答案为:110°;130°.
∴∠CDE=∠1+∠A=30°+80°=110°,
在△BCD中,∠3+∠4=180°-∠2-∠CDE=180°-30°-110°=40°,
∵∠3=∠4,
∴∠3=
| 1 |
| 2 |
在△BCE中,∠BEC=180°-∠2-∠3=180°-30°-20°=130°.
故答案为:110°;130°.
点评:本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记定理和性质并准确识图是解题的关键.

练习册系列答案
相关题目
分式
,
的最简公分母是( )
| 2 |
| a |
| 1 |
| ab |
| A、a | B、b |
| C、ab | D、a2b |
若分式
值为1,则x的值为( )
| |x|-2 |
| x-2 |
| A、x=2 | B、x≥0 |
| C、x≥2 | D、x≥0且x≠2 |
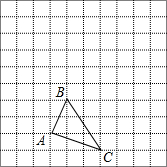 如图,已知单位长度为1的方格中有个△ABC.
如图,已知单位长度为1的方格中有个△ABC. 如图是一数值转换机,若输入的x为-5,则输出的结果为
如图是一数值转换机,若输入的x为-5,则输出的结果为