题目内容
2. 如图,AB、AC是⊙O的切线,B、C为切点,过点O作AB的平行线交AC于点D,DE⊥AB于点E.
如图,AB、AC是⊙O的切线,B、C为切点,过点O作AB的平行线交AC于点D,DE⊥AB于点E.(1)判断四边形ODEB的形状,并给予证明;
(2)将DA沿DE翻折后对应线段为DA′,判断DA′与⊙O的位置关系,证明你的结论,
(3)若tanA=$\frac{4}{3}$,AD=5.直接写出四边形ABOC的周长为24.
分析 (1)结论:四边形ODEB是矩形.首先证明四边形ODEB是平行四边形,再证明∠OBE=90°即可.
(2)结论:DA′是⊙O的切线,作OK⊥DA′于K.理由角平分线的性质定理,只要证明OK=OC即可.
(3)四边形ODEB是矩形,推出EB=OD,DE=OB,∠DEB=∠DEA=90°,设OD=EB=x,在Rt△ADE中,∵AD=5,tanA=$\frac{4}{3}$,推出DE=OB=OC=4,AE=3,由AC、AB是切线,推出AC=AB=3+x,CD=3+x-5=x-2,在Rt△CDO中,根据CD2+OC2=DO2列出方程求出x即可解决问题.
解答 解:(1)四边形ODEB是矩形.
理由:∵AB是切线,
∴OB⊥AB,∵DE⊥AB,
∴DE∥OB,
∵OD∥AB,
∴四边形ODEB是平行四边形,
∵∠OBE=90°,
∴四边形ODEB是矩形.
(2)结论:DA′是⊙O的切线,
理由:作OK⊥DA′于K.
∵DA沿DE翻折后对应线段为DA′,
∴∠ADE=∠A′DE,
∵四边形ODEB是矩形,
∴∠ODE=90°,
∴∠ODK+∠EDK=90°,∠ADE+∠CDO=90°,
∴∠ODC=∠ODK,
∵AC 是⊙O切线,
∴OC⊥DC,∵OK⊥DK,
∴OK=OC,
∴DA′是⊙O的切线.
(3)∵四边形ODEB是矩形,
∴EB=OD,DE=OB,∠DEB=∠DEA=90°,设OD=EB=x,
在Rt△ADE中,∵AD=5,tanA=$\frac{4}{3}$,
∴DE=OB=OC=4,AE=3,
∵AC、AB是切线,
∴AC=AB=3+x,CD=3+x-5=x-2,
在Rt△CDO中,∵CD2+OC2=DO2,
∴(x-2)2+42=x2,
∴x=5,
∴AB=AC=8,CO=OB=4,
∴四边形ABOC的周长为24.
故答案为24.
点评 本题考查圆综合题、矩形的判定和性质、切线的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,学会用方程的思想思考问题,属于中考压轴题.

| A. | msin40° | B. | mcos40° | C. | mtan40° | D. | $\frac{m}{tan40°}$ |
| A. | 处于中间位置的数为这组数的中位数 | |
| B. | 中间两个数的平均数为这组数的中位数 | |
| C. | 想要了解一批电磁炉的使用寿命,适合采用全面调查的方法 | |
| D. | 公司员工月收入的众数是3500元,说明该公司月收入为3500元的员工最多 |
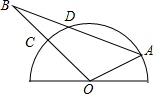 如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为105°;∠A的度数为50°.
如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为105°;∠A的度数为50°.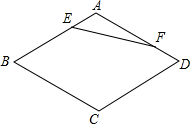 如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为$\frac{\sqrt{3}}{2}$a.
如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为$\frac{\sqrt{3}}{2}$a.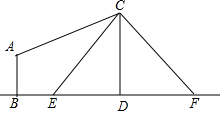 如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,求拉线CE的长,(精确到0.1米)参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.
如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,求拉线CE的长,(精确到0.1米)参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.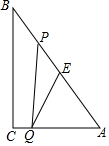 如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从 B出发沿BA向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点,点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm,当 点Q到达顶点C时,P,Q同时停止运动,设P,Q两点运动时间为t秒.
如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从 B出发沿BA向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点,点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm,当 点Q到达顶点C时,P,Q同时停止运动,设P,Q两点运动时间为t秒.