题目内容
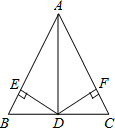 已知:D为△ABC所在平面内一点,且DB=DC,DE⊥AB,DF⊥AC,垂足分别是E、F,DE=DF.
已知:D为△ABC所在平面内一点,且DB=DC,DE⊥AB,DF⊥AC,垂足分别是E、F,DE=DF.(1)当点D在BC边上时(如图),判断△ABC的形状(直接写出答案);
(2)当点D在△ABC内部时,(1)中的结论是否一定成立?若成立,请证明;若不成立,请举出反例(画图说明).
(3)当点D在△ABC外部时,(1)中的结论是否一定成立?若成立,请证明;若不成立,请举出反例(画图说明).
考点:等腰三角形的判定,全等三角形的判定与性质
专题:
分析:(1)用(HL)证明△EBD≌△FCD,从而得出∠EBD=∠FCD,即可证明△ABC是等腰三角形;(2)先画图,根据已知可证明△EBD≌△FCD,从而得出∠EBD=∠FCD,由DB=DC,可得∠DBC=∠DCB,从而可得∠EBD=∠FCD,即可证明△ABC是等腰三角形;(3)通过画图可知当点D在在△ABC外部时,(1)中的结论不一定成立,
解答:解:(1)△ABC是等腰三角形.
证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,且DE=DF,
∵DB=DC,
在Rt△EBD与Rt△FCD中,
∴Rt△EBD≌Rt△FCD(HL),
∴∠EBD=∠FCD,
∴AB=AC,
∴△ABC是等腰三角形.
(2)如图,当点D在△ABC内部时,△ABC是等腰三角形成立,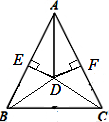
理由:∵DE⊥AB,DF⊥AC
∴∠BED=∠CFD=90°,且DE=DF,
∵DB=DC,
在Rt△EBD与Rt△FCD中,
∴Rt△EBD≌Rt△FCD(HL),
∴∠EBD=∠FCD,
∵DB=DC,
∴∠DBC=∠DCB,
∴∠EBD+∠DBC=∠FCD+∠DCB,
即∠EBD=∠FCD,
∴AB=AC,
∴△ABC是等腰三角形;
(3)当点D在在△ABC外部时,(1)中的结论不一定成立,
反例如图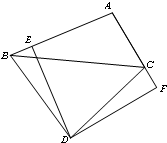 :
:
证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,且DE=DF,
∵DB=DC,
在Rt△EBD与Rt△FCD中,
|
∴Rt△EBD≌Rt△FCD(HL),
∴∠EBD=∠FCD,
∴AB=AC,
∴△ABC是等腰三角形.
(2)如图,当点D在△ABC内部时,△ABC是等腰三角形成立,

理由:∵DE⊥AB,DF⊥AC
∴∠BED=∠CFD=90°,且DE=DF,
∵DB=DC,
在Rt△EBD与Rt△FCD中,
|
∴Rt△EBD≌Rt△FCD(HL),
∴∠EBD=∠FCD,
∵DB=DC,
∴∠DBC=∠DCB,
∴∠EBD+∠DBC=∠FCD+∠DCB,
即∠EBD=∠FCD,
∴AB=AC,
∴△ABC是等腰三角形;
(3)当点D在在△ABC外部时,(1)中的结论不一定成立,
反例如图
 :
:点评:本题主要考查三角形全等的判定、性质及学等腰三角形的判定方法,证明此题的关键是用(HL)证明△EBD≌△FCD,从而得出∠EBD=∠FCD,即可证明△ABC是等腰三角形.

练习册系列答案
相关题目
 如图,将一副三角尺按不同位置摆放,在哪种摆放方式中∠α与∠β互余?在哪种摆放方式中∠α与∠β互补?在哪种摆放方式中∠α与∠β相等?
如图,将一副三角尺按不同位置摆放,在哪种摆放方式中∠α与∠β互余?在哪种摆放方式中∠α与∠β互补?在哪种摆放方式中∠α与∠β相等? 如图,已知直线AB,CD相交于点O,EO⊥AB于点O,且∠DOE=8∠COE,求∠BOC和∠BOD的度数.
如图,已知直线AB,CD相交于点O,EO⊥AB于点O,且∠DOE=8∠COE,求∠BOC和∠BOD的度数. 如图,一个反比例函数的图象与△OAB的边AB相交,已知AB与y轴平行,A点坐标为(4,4),若△OAB的面积为3,这个反比例函数的表达式为
如图,一个反比例函数的图象与△OAB的边AB相交,已知AB与y轴平行,A点坐标为(4,4),若△OAB的面积为3,这个反比例函数的表达式为 在平行四边形ABCD的对角线AC上截取AE=CF,作EH⊥BC,FG⊥AD.求证:GH与EF互相平分.
在平行四边形ABCD的对角线AC上截取AE=CF,作EH⊥BC,FG⊥AD.求证:GH与EF互相平分. 如图所示:在△ABC中,AD为BC边上的中线,AC=
如图所示:在△ABC中,AD为BC边上的中线,AC= 如图,梯形ABCD中,AD∥BC,∠ABC+∠BCD=90°,且BC=3AD,分别以BA、AD、DC为边向梯形外作正方形,其面积分别为S1,S2,S3,则S1,S2,S3之间的关系是
如图,梯形ABCD中,AD∥BC,∠ABC+∠BCD=90°,且BC=3AD,分别以BA、AD、DC为边向梯形外作正方形,其面积分别为S1,S2,S3,则S1,S2,S3之间的关系是 如图,已知∠1=∠2,BD平分∠ABC.
如图,已知∠1=∠2,BD平分∠ABC.