Question

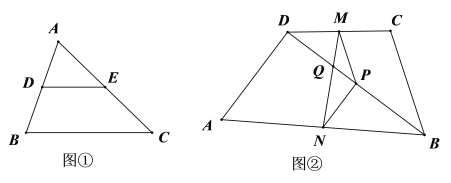
【题目】教材呈现：下图是华师版九年级上册数学教材第77页的部分内容.

猜想：

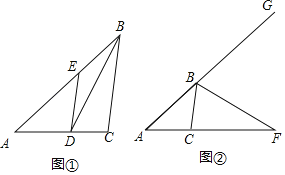
如图，在中，点分别是与的中点，根据画出的图形，可以猜想：

，且.

对此，我们可以用演绎推理给出证明.

证明：在中，

∵点分别是与的中点，

∴.

请根据教材提示，结合图①，写出完整的证明过程.

结论应用：

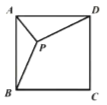
如图②在四边形中，，点是对角线的中点，是中点，是中点，与相交于点.

（1）求证：；

（2）若，，，则_______________.

Answer 1

【答案】猜想：证明过程见解析；结论应用：（1）见解析；（2）.

【解析】

猜想：利用两边对应成比例且夹角相等可证，再利用相似三角形的性质即可证得猜想；

结论应用：（1）根据猜想的结论可得：，，进而可得，然后利用等腰三角形的性质即可得出结论；

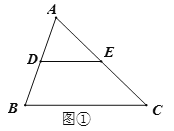
（2）过点P作PF⊥MN于点F，如图②，由（1）得：PN∥AD，PM∥BC，然后利用平行线的性质即可求出∠MPN，再由（1）的结论可得∠2的度数，因为，而BC=4，所以MP=2，因为∠PQF=∠1+∠2，所以∠PQF可得，然后在直角△PQF中利用30°角的直角三角形的性质即可求出结果.

教材呈现：

证明：在中，∵点分别是与的中点，

∴，

∵，∴，

∴，，

∴，.

结论应用：

（1）证明：∵分别为的中点，∴，

∵分别为的中点，∴，

∵，∴，

∴；

（2）解：过点P作PF⊥MN于点F，如图②，

由（1）得：PN∥AD，PM∥BC，

∴∠NPB=∠ADB=90°=∠NPD，∠1=∠DBC=30°，∴∠MPN=30°+90°=120°，

∵，∴，

∵，，，

∴，

∴PF=，

∵∠PQF=∠1+∠2=60°，∴∠QPF=30°，

∴，

∴.

故答案为：.