题目内容
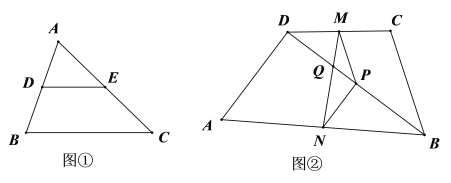
【题目】探究:如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥BC交AB于点E,AB=5,BC=3,求![]() 的值.
的值.
应用:如图②,在△ABC中,BF是△ABC的外角的平分线,交AC的延长线于点F,AB=5,BC=3,则![]() =______.
=______.
【答案】探究:![]() ;应用:
;应用:![]() .
.
【解析】
探究:通过证明△ADE∽△ACB,可求AE的长,即可求解;
应用:过点F作FH∥BC,交AG于H点,通过证明△ABC∽△AHF,可求BH的长,即可求解.
探究:
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵DE∥BC,
∴∠EDB=∠DBC,
∴∠EDB=∠ABD,
∴DE=BE,
∵DE∥BC,
∴△ADE∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴AE=![]() ,
,
∴BE=![]() ,
,
∵DE∥BC,
∴![]() ,
,
∴![]() ;
;
应用:
如图,过点F作FH∥BC,交AG于H点,

∵FH∥BC,
∴∠CBF=∠BFH,
∵BF平分∠HBC,
∴∠CBF=∠HBF,
∴∠BFH=∠HBF,
∴HF=BH,
∵FH∥BC,
∴△ABC∽△AHF,
∴![]() ,
,
∴![]()
∴BH=![]() ,
,
∵FH∥BC,
∴![]() =
=![]() =
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目