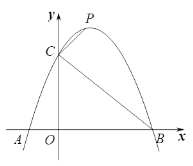题目内容

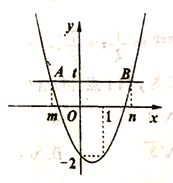
【题目】如图为二次函数图象，直线与抛物线交于两点,两点横坐标分别为根据函数图象信息有下列结论:

①;

②若对于的任意值都有,则;

③;

④;

⑤当为定值时若变大,则线段变长

其中，正确的结论有__________(写出所有正确结论的番号)

【答案】①②③

【解析】

分别参考图像去解答，因为对称轴为正数，所以 异号，根据与y轴交点为c得出,去判断各种情况，而且越大开口越小，进而得出正确答案即可.

解：①中，对称轴为正数，所以 异号，

与y轴交点为，

，

，故①对；

②中，由图像得：，知道,

当函数与x轴左交点为时，代入函数表达式得：

,

,此时考虑的是临界情况，

对于的任意值都有,则，故②对；

③中，所对的值是关于对称轴对称的，

对称轴,

,故③对；

④中无法确定；

⑤中，当为定值时若变大,则抛物线的开口变小，则线段变短，故⑤错；

故答案填：①②③.

练习册系列答案
相关题目

【题目】如图，已知动点A在函数的图象上，AB⊥x轴于点B，AC⊥y轴于点C，延长CA交以A为圆心AB长为半径的圆弧于点E，延长BA交以A为圆心AC长为半径的圆弧于点F，直线EF分别交x轴、y轴于点M、N，当NF＝4EM时，图中阴影部分的面积等于_____．

【题目】如图，在中，点，点在轴正半轴上，以为一边作等腰直角，使得点在第一象限．

（1）求出所有符合题意的点的坐标；

（2）在内部存在一点，使得之和最小，请求出这个和的最小值．

【题目】（方法回顾）

课本研究三角形中位线性质的方法

已知：如图①， 已知中，，分别是，两边中点．

求证：，

证明：延长至点，使， 连按．可证：（　　）

由此得到四边形为平行四边形， 进而得到求证结论

（1）请根据以上证明过程，解答下列两个问题：

①在图①中作出证明中所描述的辅助线（请用铅笔作辅助线）；

②在证明的括号中填写理由（请在，，，中选择） .

（问题拓展）

（2）如图②，在等边中， 点是射线上一动点（点在点的右侧），把线段绕点逆时针旋转得到线段，点是线段的中点，连接、．

①请你判断线段与的数量关系，并给出证明；

②若，求线段长度的最小值．

【题目】甲、乙两车沿同一条道路从地出发向1200外的地输送紧急物资，甲在途中休息了3小时，休息前后的速度不同，最后两车同时到达地，如图甲、乙两车到地的距离（千米）与乙车行驶时间（小时）之间的函数图象．

（1）甲车休息前的行驶速度为 千米/时，乙车的速度为 千米/时；

（2）当9≤≤15，求甲车的行驶路程与之间的函数关系式；

（3）直接写出甲出发多长时间与乙在途中相遇．

【题目】如图，已知二次函数的图像与x轴交于A、B两点(点A在点B左侧)，与y轴交于点C.

(1)求线段BC的长；

(2)当0≤y≤3时，请直接写出x的范围；

(3)点P是抛物线上位于第一象限的一个动点，连接CP，当∠BCP＝90o时，求点P的坐标.

【题目】抛物线（为常数，）与轴交于，两点，与轴交于点．设该抛物线的顶点为，其对称轴与轴的交点为．

（1）求该抛物线的解析式；

（2）为线段（含端点）上一点，为轴上一点，且．

①求的取值范围；

②当取最大值时，将线段向上平移个单位长度，使得线段与抛物线有两个交点，求的取值范围．

【题目】已知中，，（如图）．以线段为边向外作等边三角形，点是线段的中点，连接并延长交线段于点．

（1）求证：四边形为平行四边形；

（2）连接，交于点．

①若，求的长；

②作，垂足为，求证：．

【题目】小超骑电动车、小生骑自行车分别同时从甲、乙两地出发，匀速相向而行，在分钟时两人相遇，在行驶的过程中，小超到达乙地后停留一会，再按原路原速返回甲地，小生一直匀速骑自行车后，与小超同时到达甲地，如图表示两人距乙地的距离与时间之间的函数关系．

（1）小超骑车的速度_ ，小生骑车的速度 ；

（2）求线段的解析式；

（3）如果小超不在乙地停留，按原路原速直接返回，问在小超回到甲地之前，小超何时能追上小生？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网