题目内容
11. 甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
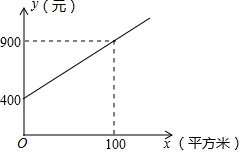
甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500 元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.
(1)求如图所示的y与x的函数解析式:(不要求写出定义域);
(2)如果某学校目前的绿化面积是1200平方米,试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
分析 (1)利用待定系数法即可解决问题;
(2)绿化面积是1200平方米时,求出两家的费用即可判断;
解答 解:(1)设y=kx+b,则有$\left\{\begin{array}{l}{b=400}\\{100k+b=900}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=5}\\{b=400}\end{array}\right.$,
∴y=5x+400.
(2)绿化面积是1200平方米时,甲公司的费用为6400元,乙公司的费用为5500+4×200=6300元,
∵6300<6400
∴选择乙公司的服务,每月的绿化养护费用较少.
点评 本题主要考查一次函数的应用.此题属于图象信息识别和方案选择问题.正确识图是解好题目的关键.

练习册系列答案
相关题目
2.下列运算正确的是( )
| A. | -3(x-4)=-3x+12 | B. | (-3x)2•4x2=-12x4 | C. | 3x+2x2=5x3 | D. | x6÷x2=x3 |
19.如果一次函数y=kx+b(k、b是常数,k≠0)的图象经过第一、二、四象限,那么k、b应满足的条件是( )
| A. | k>0,且b>0 | B. | k<0,且b>0 | C. | k>0,且b<0 | D. | k<0,且b<0 |
16. 某几何体的左视图如图所示,则该几何体不可能是( )
某几何体的左视图如图所示,则该几何体不可能是( )
 某几何体的左视图如图所示,则该几何体不可能是( )
某几何体的左视图如图所示,则该几何体不可能是( )| A. |  | B. |  | C. |  | D. |  |
9.郴州市某景区的门票其票价如下:
今有甲乙两个旅游团均超过40人,且甲团人数少于乙团人数,两个团合在一起购票,总计付出门票费10080元.
(1)这两个旅游团共有多少人?
(2)若两旅游团分别购票,总计应付门票13140元,请问甲,乙两个旅游团各有多少人?
| 购票人数 | 1~49人 | 50~100人 | 100人以上 |
| 每人门票价 | 130元 | 110元 | 90元 |
(1)这两个旅游团共有多少人?
(2)若两旅游团分别购票,总计应付门票13140元,请问甲,乙两个旅游团各有多少人?