题目内容
9. 如图,在四边形纸片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°.将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平.若铺平后的图形中有一个是面积为2的平行四边形,则CD=2+$\sqrt{3}$或4+2$\sqrt{3}$.
如图,在四边形纸片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°.将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平.若铺平后的图形中有一个是面积为2的平行四边形,则CD=2+$\sqrt{3}$或4+2$\sqrt{3}$.
分析 根据题意结合裁剪的方法得出符合题意的图形有两个,分别利用菱形的判定与性质以及勾股定理得出CD的长.
解答 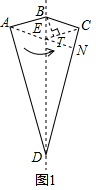 解:如图1所示:作AE∥BC,延长AE交CD于点N,过点B作BT⊥EC于点T,
解:如图1所示:作AE∥BC,延长AE交CD于点N,过点B作BT⊥EC于点T,
当四边形ABCE为平行四边形,
∵AB=BC,
∴四边形ABCE是菱形,
∵∠A=∠C=90°,∠B=150°,BC∥AN,
∴∠ADC=30°,∠BAN=∠BCE=30°,
则∠NAD=60°,
∴∠AND=90°,
∵四边形ABCE面积为2,
∴设BT=x,则BC=EC=2x,
故2x×x=2,
解得:x=1(负数舍去),
则AE=EC=2,EN=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
故AN=2+$\sqrt{3}$,
则AD=DC=4+2$\sqrt{3}$;
如图2,当四边形BEDF是平行四边形,
∵BE=BF,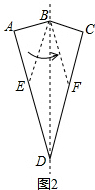
∴平行四边形BEDF是菱形,
∵∠A=∠C=90°,∠B=150°,
∴∠ADB=∠BDC=15°,
∵BE=DE,
∴∠AEB=30°,
∴设AB=y,则BE=2y,AE=$\sqrt{3}$y,
∵四边形BEDF面积为2,
∴AB×DE=2y2=2,
解得:y=1,故AE=$\sqrt{3}$,DE=2,
则AD=2+$\sqrt{3}$,
综上所述:CD的值为:2+$\sqrt{3}$或4+2$\sqrt{3}$.
故答案为:2+$\sqrt{3}$或4+2$\sqrt{3}$.
点评 此题主要考查了剪纸问题以及勾股定理和平行四边形的性质等知识,根据题意画出正确图形是解题关键.

练习册系列答案
相关题目
19.下列式子中是一元一次方程的是( )
| A. | x2-3=0 | B. | $\frac{x}{5}$+2=11 | C. | x-y=1 | D. | x-2=$\frac{3}{x}$ |
20.下列各组长度的线段中,不能够组成三角形的是( )
| A. | 1cm,2cm,3cm | B. | 3cm,4cm,5cm | C. | 5cm,6cm,7cm | D. | 7cm,8cm,9cm |
4.中学生骑电动车上学给交通安全带来隐患,为了解某中学2500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法错误的是( )
| A. | 调查方式是抽样调查 | |
| B. | 该校只有360个家长持反对态度 | |
| C. | 样本是400个家长对“中学生骑电动车上学”的态度 | |
| D. | 该校约有90%的家长持反对态度 |
 如图,已知在等边三角形ABC中,AD⊥BC,AD=AC,联结CD并延长,交AB的延长线于点E,求∠E的度数.
如图,已知在等边三角形ABC中,AD⊥BC,AD=AC,联结CD并延长,交AB的延长线于点E,求∠E的度数.
 阅读材料:
阅读材料: 如图,将?ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.
如图,将?ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.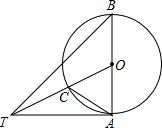 如图,AB是⊙O的直径,∠ABT=45°,AT=AB.
如图,AB是⊙O的直径,∠ABT=45°,AT=AB.