题目内容
9.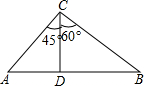 如图,在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,AC=$40\sqrt{2}$,求AB.
如图,在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,AC=$40\sqrt{2}$,求AB.
分析 根据在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,AC=$40\sqrt{2}$,可以求得∠CDA=∠CDB=90°,从而可以求得各边的长,本题得以解决.
解答 解:∵在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,
∴∠CDA=∠CDB=90°,∠CAD=45°,∠B=30°,
∴CD=AD,BC=2CD,
∵AC=$40\sqrt{2}$,CD2+AD2=AC2,
∴CD=AD=$\sqrt{\frac{A{C}^{2}}{2}}=\sqrt{\frac{(40\sqrt{2})^{2}}{2}}$=40,
∴BC=80,
∴BD=$\sqrt{B{C}^{2}-C{D}^{2}}=\sqrt{8{0}^{2}-4{0}^{2}}=40\sqrt{3}$,
∴AB=AD+BD=40+40$\sqrt{3}$,
即AB的长是40+40$\sqrt{3}$.
点评 本题考查解直角三角形,解题的关键是明确各边之间的关系,由题目中的信息求出各边的长,然后找出所求问题需要的条件.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
19.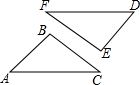 如图,△ABC≌△DEF,∠A=50°,∠B=100°,则∠F的度数是( )
如图,△ABC≌△DEF,∠A=50°,∠B=100°,则∠F的度数是( )
 如图,△ABC≌△DEF,∠A=50°,∠B=100°,则∠F的度数是( )
如图,△ABC≌△DEF,∠A=50°,∠B=100°,则∠F的度数是( )| A. | 30° | B. | 50° | C. | 60° | D. | 100° |
17.八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
①甲队成绩的中位数是9.5分,乙队成绩的众数是10 分;
②计算乙队的平均成绩和方差.
| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
②计算乙队的平均成绩和方差.
18.抛物线y=ax2+bx+c(a≠0)上部分点的横、纵坐标的对应值如下表:
则该抛物线的顶点坐标为(2,-4).
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 14 | 4 | -2 | -4 | -2 | 4 | … |
19.下列事件是确定事件的是( )
| A. | 任意打开一本200页的数学书,恰好是第50页 | |
| B. | 打开电视机,任选一个频道,正在播放足球赛 | |
| C. | 在空旷的操场上向上抛出的篮球一定会下落 | |
| D. | 阴天一定会下雨 |