题目内容
17．八（2）班组织了一次经典朗读比赛，甲、乙两队各10人的比赛成绩如下表（10分制）：| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
②计算乙队的平均成绩和方差．
分析 （1）根据中位数的定义求出最中间两个数的平均数；根据众数的定义找出出现次数最多的数即可；
（2）先求出乙队的平均成绩，再根据方差公式进行计算．
解答 解：①把甲队的成绩从小到大排列为：7，7，8，9，9，10，10，10，10，10，最中间两个数的平均数是（9+10）÷2=9.5（分），
则中位数是9.5分；
乙队成绩中10出现了4次，出现的次数最多，
则乙队成绩的众数是10分；
故答案为：9.5，10；
②乙队的平均成绩是：$\frac{1}{10}$×（10×4+8×2+7+9×3）=9，
则方差是：$\frac{1}{10}$×[4×（10-9）2+2×（8-9）2+（7-9）2+3×（9-9）2]=1．
点评 本题考查方差、中位数和众数，关键是根据中位数、方差和中位数的定义解答．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．下面说法错误的是（ ）
| A． | 两点确定一条直线 | B． | 射线AB也可以写作射线BA | ||
| C． | 等角的余角相等 | D． | 同角的补角相等 |
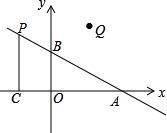如图，在平面直角坐标系中，O是坐标原点，点A的坐标为（4，0），点B的坐标为（0，b）（b＞0），点P是直线AB上位于第二象限内的一个动点，过点P作PC⊥x轴于点C，记点P关于y轴的对称点为Q，设点P的横坐标为a．
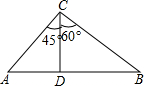如图，在△ABC中，CD⊥AB，∠ACD=45°，∠DCB=60°，AC=$40\sqrt{2}$，求AB．
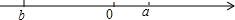已知有理数a，b在数轴上的位置如图所示．