题目内容
18.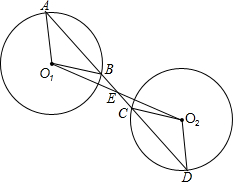 如图所示,⊙O1和⊙O2为两个等圆,O1A∥O2D,O1O2与AD相交于点E,AD与⊙O1和⊙O2分别交于点B,C,求证:AB=CD.
如图所示,⊙O1和⊙O2为两个等圆,O1A∥O2D,O1O2与AD相交于点E,AD与⊙O1和⊙O2分别交于点B,C,求证:AB=CD.
分析 分别过O1,O2作O1G⊥AB,O2H⊥CD垂足分别为G,H,由已知条件易证∴△O1GE≌△O2HE(AAS),所以O1G=O2H,进而可证明:AB=CD(同圆或等圆中,相等的弦心距所对的弦相等).
解答 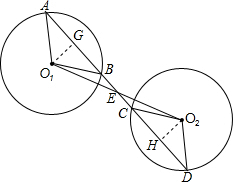 证明:分别过O1,O2作O1G⊥AB,O2H⊥CD垂足分别为G,H,
证明:分别过O1,O2作O1G⊥AB,O2H⊥CD垂足分别为G,H,
∴∠O1GE=∠O2HE=90°,
∵O1A∥O2D,
∴∠A=∠D,
在△O1AE和△O2DE中,
$\left\{\begin{array}{l}{∠A=∠D}\\{∠{O}_{1}EA=∠{O}_{2}ED}\\{{O}_{1}A={O}_{2}D}\end{array}\right.$,
∴△O1AE≌△O2DE(AAS),
∴O1E=O2E,
在△O1GE和△O2HE中,
$\left\{\begin{array}{l}{∠{O}_{1}EG=∠{O}_{2}EH}\\{∠{O}_{1}GE=∠{O}_{2}HE=90°}\\{{O}_{1}E={O}_{2}E}\end{array}\right.$,
∴△O1GE≌△O2HE(AAS),
∴O1G=O2H,
∴AB=CD(同圆或等圆中,相等的弦心距所对的弦相等).
点评 本题考查了圆与圆的位置关系,全等三角形的判断和性质以及圆心定理,题目的综合性较强,难度不大,是中考常见题型.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
9.有一种长方体集装箱,其内空长为5米,高4.5米,宽3.4米,用这样的集装箱运长为5米,横截面的外圆直径为0.8米的圆柱形钢管,最多能运( )根.
| A. | 20根 | B. | 21根 | C. | 24根 | D. | 25根 |
3.根据2010年第六次全国人口普查主要数据公报,广东省常住人口约为10430万人.这个数据可以用科学记数法表示为( )
| A. | 1.043×108人 | B. | 1.043×107人 | C. | 1.043×104人 | D. | 1043×105人 |
10.用配方法解方程x2+4x-6=0,下列配方正确的是( )
| A. | (x+4)2=22 | B. | (x+2)2=10 | C. | (x+2)2=8 | D. | (x+2)2=6 |
8.若(x2+m)(x2+$\frac{1}{3}$)中不含x2项,则m的值为( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -$\frac{1}{3}$ | D. | -3 |

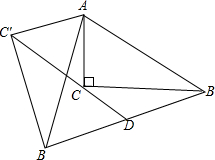 在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转,B、C旋转后的对应点分别是B′和C′.连接C′C并延长交B′B于点D.
在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转,B、C旋转后的对应点分别是B′和C′.连接C′C并延长交B′B于点D.