题目内容
4.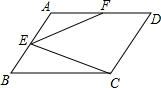 如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°)
如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°)(1)当α=60°时,求CE的长;
(2)当60°<α<90°时,
①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.(友情提示:连接CF并延长,交BA延长线于点G)
②当E为AB中点时,连接CF,求tan∠DCF的值.
分析 (1)在直角△BCE中利用三角函数即可求解;
(2)①连接CF并延长交BA的延长线于点G,证明△AFG≌△CFD得到CF=GF,AG=CD,在△AFG中利用外角的性质即可求解;
②连接CF并延长交BA的延长线于点G,利用三角函数的定义即可求解.
解答 解:(1)∵在直角△BCE中,sin∠ABC=$\frac{CE}{BC}$,
∴CE=5$\sqrt{3}$;
(2)①存在k=3,使得∠EFD=k∠AEF.
理由如下:
连接CF并延长交BA的延长线于点G,
∵F为AD的中点,
∴AF=FD.
在平行四边形ABCD中,AB∥CD,
∴∠G=∠DCF.
在△AFG和△CFD中,
∵$\left\{\begin{array}{l}{∠G=∠DCF}\\{∠AFG=∠DFC}\\{AF=FD}\end{array}\right.$,
∴△AFG≌△CFD(AAS).
∴CF=GF,AG=CD.
∵CE⊥AB,F是GC边中点.
∴EF=GF.
∴∠AEF=∠G.
∵AB=5,BC=10,点F是AD的中点,
∴AG=5,AF=AD=BC=5.
∴AG=AF.
∴∠AFG=∠G.
在△AFG中,∠EFC=∠AEF+∠G=2∠AEF,
又∵∠CFD=∠AFG,
∴∠CFD=∠AEF.
∴∠EFD=∠EFC+∠CFD=2∠AEF+∠AEF=3∠AEF,
因此,存在正整数k=3,使得∠EFD=3∠AEF.
(2)连接CF并延长交BA的延长线于点G,
在直角△BCE中,BC=10,BE=$\frac{1}{2}$AB=$\frac{5}{2}$,
则CE=$\sqrt{B{C}^{2}-B{E}^{2}}$=$\sqrt{1{0}^{2}-(\frac{5}{2})^{2}}$=$\frac{5\sqrt{15}}{2}$,
∵F为AD的中点,AF∥BC,
∴A是BG的中点,则BG=2AB=10,
∴EG=BG-BE=10-$\frac{5}{2}$=$\frac{15}{2}$.
又∵AB∥CD,
∴∠DCF=∠G,
∴tan∠DCF=tan∠G=$\frac{CE}{GE}$=$\frac{5\sqrt{15}}{15}$=$\frac{\sqrt{15}}{3}$.
点评 本题是全等三角形的判定与性质以及三角函数和三角形的外角的性质的综合应用,正确作出辅助线是关键.

| A. | 扩大4倍 | B. | 扩大2倍 | C. | 不变 | D. | 缩小2倍 |
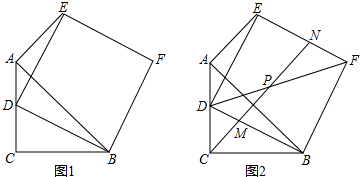
 如图,∠B=∠ADC=90°,AD=2DC,AB=BC=$\sqrt{6}$cm,求四边形ABCD的面积.
如图,∠B=∠ADC=90°,AD=2DC,AB=BC=$\sqrt{6}$cm,求四边形ABCD的面积.