题目内容
9.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC,D为AC边上一点,以BD为边作正方形BDEF.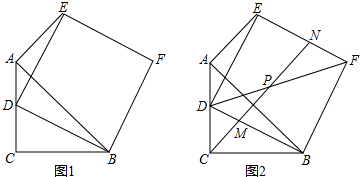
(1)求证:AE⊥AB;
(2)如图2,P为正方形BDEF的对角线的中点,直线CP分别交BD、EF于M、N两点.
①求证:△BCM∽△PFN;
②若$\frac{DC}{AD}=\frac{2}{3}$,则$\frac{EN}{FN}$=$\frac{5}{2}$.(直接写出结果,不需要过程)
分析 (1)连接BE,由正方形的性质和等腰直角三角形的性质可得∠EBA=∠DBC,且$\frac{EB}{DB}$=$\frac{AB}{BC}$=$\sqrt{2}$,可证明△EBA∽△DBC,则可知AE⊥AB;
(2)①连接BE、AP,可证明PC垂直平分AB,可求得∠CBG=∠MCB=45°,再结合正方形的性质可得∠CMB=∠PNF,可证明△BCM∽△PFN;②在△BCD中,由角平分线的性质可得$\frac{BC}{CD}$=$\frac{BM}{DM}$,结合正方形的性质可知$\frac{BM}{DM}$=$\frac{EN}{FN}$,可求得答案.
解答 (1)证明:
如图1,连接BE,
在正方形EDBF中,ED=BD,∠EBD=45°,
在等腰Rt△ABC中,AC=BC,∠ABC=45°,
∴∠EBA=∠DBC,且$\frac{EB}{DB}$=$\frac{AB}{BC}$=$\sqrt{2}$,
∴△EBA∽△DBC,
∴∠EAB=∠DCB=90°,
∴AE⊥AB;
(2)①证明:
如图2,连接BE、AP,
∵在正方形BDEF中,DF、BE互相平分,
∴BE过点P,
由(1)知∠EAB=90°,则在Rt△EAB中,点P为BE中点,
∴AP=BP,
∵AC=BC,
∴PC垂直平分AB,
∴∠CGB=90°,
∵∠CBG=45°,
∴∠MCB=45°,
∵在正方形BDEF中,BD∥EF,
∴∠CMB=∠PNF,
∵∠BCM=∠PFN=45°,∠CMB=∠PNF,
∴△BCM∽△PFN;
②由①可知CM平分∠DCB,
∴$\frac{BC}{CD}$=$\frac{BM}{DM}$,
在△DMP和△FNP中
$\left\{\begin{array}{l}{∠DPM=∠FPN}\\{PD=PF}\\{∠PDM=∠PFN}\end{array}\right.$
∴△DMP≌△FNP(ASA),
∴DM=FN,则BM=EN,
∴$\frac{BM}{DM}$=$\frac{EN}{FN}$,
∵$\frac{CD}{AD}$=$\frac{2}{3}$,
∴$\frac{AC}{CD}$=$\frac{5}{2}$,
又AC=BC,
∴$\frac{BC}{CD}$=$\frac{5}{2}$,
∴$\frac{EN}{FN}$=$\frac{5}{2}$,
故答案为:$\frac{5}{2}$.
点评 本题主要考查相似三角形的判定和性质及正方形的性质、角平分线的性质等知识的综合应用.在(1)中连接BE构造相似三角形是解题的关键,在(2)中证得PC垂直平分AB是解题的关键.本题目综合性质较强,考查知识点较多,难度较大,特别是在复杂图形中寻找出相似三角形,更是考查了对知识的熟练掌握.

 阅读快车系列答案
阅读快车系列答案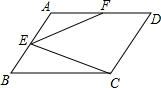 如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°)
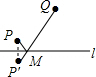
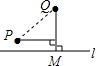
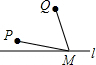
如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°)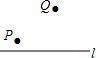 如图,直线1表示石家庄的太平河,点P表示朱河村,点Q表示黄庄村,欲在太平河1上修建一个水泵站(记为点M),分别向两村供水,现有如下四种修建水泵站供水管道的方案,图中实线表示修建的管道,则修建的管道最短的方案是( )
如图,直线1表示石家庄的太平河,点P表示朱河村,点Q表示黄庄村,欲在太平河1上修建一个水泵站(记为点M),分别向两村供水,现有如下四种修建水泵站供水管道的方案,图中实线表示修建的管道,则修建的管道最短的方案是( )
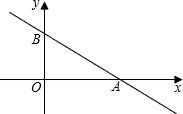 如图,直线y=kx+3与x轴、y轴分别交于A、B两点,$\frac{OB}{OA}$=$\frac{3}{4}$,点C是直线y=kx+3上与A、B不重合的动点,过点C的另一直线CD与y轴相交于点D,是否存在点C使△BCD与△AOB全等?若存在,求出点C的坐标;若不存在,请说明理由.
如图,直线y=kx+3与x轴、y轴分别交于A、B两点,$\frac{OB}{OA}$=$\frac{3}{4}$,点C是直线y=kx+3上与A、B不重合的动点,过点C的另一直线CD与y轴相交于点D,是否存在点C使△BCD与△AOB全等?若存在,求出点C的坐标;若不存在,请说明理由.