题目内容
15.在Rt△ABC中,∠C=90°,BC=6,sinB=$\frac{3}{5}$,试分别求出AC、AB的值.分析 在Rt△ABC中,由sinB=$\frac{3}{5}$,设AC=3k,AB=5k,由勾股定理列方程即可得到结论.
解答 解:在Rt△ABC中,∠C=90°,BC=6,sinB=$\frac{3}{5}$,
设AC=3k,AB=5k,
由勾股定理得:AC2+BC2=AB2,
即(3k)2+62=(5k)2,
解得:k=$\frac{3}{2}$,
则AC=$\frac{9}{2}$,AB=$\frac{15}{2}$.
点评 此题主要考查了锐角三角函数关系以及勾股定理,正确掌握锐角三角函数关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.某乡有四个村生产草莓,每千克售2.25元.填表:(用计算器计算)
| 村别 | 甲村 | 乙村 | 丙村 | 丁村 | 四村合计 |
| 数量(kg) | 12560 | 8974 | 9670 | 8796 | 40000 |
| 金额(元) | 28260 | 20191.5 | 21757.5 | 19791 | 90000 |
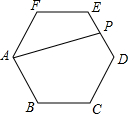 如图,在正六边形ABCDEF中,AB=2,P是ED的中点,连接AP,求AP的长.
如图,在正六边形ABCDEF中,AB=2,P是ED的中点,连接AP,求AP的长. 如图,在△ABC中,AB=AC,AD和BE是高,它们交于点H,且AE=BE.求证:
如图,在△ABC中,AB=AC,AD和BE是高,它们交于点H,且AE=BE.求证: 如图,A(3,0),B(0,3),C(1,4),求△ABC的面积.
如图,A(3,0),B(0,3),C(1,4),求△ABC的面积.