题目内容
请写出一个一元二次方程,要求满足下列两个条件:①有两个不相等的实数根;②其中有一个根为x=2,所写的方程是 .
考点:根的判别式
专题:开放型
分析:设方程另一个根为0,则满足条件的方程为x(x-2)=0,然后整理为一般式即可.
解答:解:根据题意得x(x-2)=0,
即x2-2x=0.
故答案为x2-2x=0.
即x2-2x=0.
故答案为x2-2x=0.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
已知a<b,则下列各式不成立的是( )
| A、3a<3b |
| B、-3a<-3b |
| C、a-3<b-3 |
| D、3+a<3+b |
-27的立方根与
的算术平方根的和是( )
| 81 |
| A、0 | B、6 |
| C、6或-12 | D、0或6 |
 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,EC=8,
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,EC=8,| AD |
| BD |
| 3 |
| 4 |
A、
| ||
| B、6 | ||
C、
| ||
| D、5.5 |
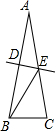 如图,等腰三角形ABC中,AB=AC,∠A=20°,线段AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE等于( )
如图,等腰三角形ABC中,AB=AC,∠A=20°,线段AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE等于( )| A、80° | B、70° |
| C、50° | D、60° |