题目内容
3.如图,点O是半径为2的圆形纸片的圆心,将这个圆形纸片按下列顺序折叠,使和弧BC都经过圆心O,则阴影部分的面积是$\frac{4π}{3}$.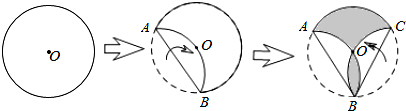
分析 作OD⊥AB于点D,连接AO,BO,CO,求出∠OAD=30°,得到∠AOB=2∠AOD=120°,进而求得∠AOC=120°,再利用阴影部分的面积=S扇形AOC得出阴影部分的面积是⊙O面积的$\frac{1}{3}$,即可得出结果.
解答 解:作OD⊥AB于点D,连接AO,BO,CO,如图所示: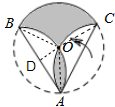
∵OD=$\frac{1}{2}$AO
∴∠OAD=30°,
∴∠AOB=2∠AOD=120°,
同理∠BOC=120°,
∴∠AOC=120°,
∴阴影部分的面积=S扇形BOC=$\frac{1}{3}$×⊙O面积=$\frac{1}{3}$×π×22=$\frac{4π}{3}$;
故答案为:$\frac{4π}{3}$.
点评 本题主要考查了翻折变换的性质、扇形面积以及圆的面积公式等知识;解题的关键是确定∠AOC=120°.

练习册系列答案
相关题目
13.下列方程的变形,符合等式的性质的是( )
| A. | 由2x-3=7,得2x=7-3 | B. | 由3x-2=x+1,得3x-x=1-2 | ||
| C. | 由-2x=5,得x=-3 | D. | 由-$\frac{1}{3}$x=1,得x=-3 |
18.若反比例函数y=$\frac{k+2}{x}$的图象位于第二、四象限,则k的取值范围可能是( )
| A. | -3 | B. | -1 | C. | 0 | D. | 1 |
12.⊙O的半径为1,同一平面内,若点P与圆心O的距离为1,则点P与⊙O的位置关系是( )
| A. | 点P在⊙O外 | B. | 点P在⊙O上 | C. | 点P在⊙O内 | D. | 无法确定 |
13.|-3|等于( )
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | -3 |