题目内容
已知梯形ABCD中，AB∥CD，过点C作CE∥AD，交AB于点E．（1）请判断∠A与∠DCE的数量关系，并说明理由；
（2）设∠A=（3x-24）°，∠DCE=（56-x）°，求∠D的度数．
考点：梯形
专题：
分析：（1）由AB∥CD，CE∥AD就可以得出四边形AECD是平行四边形，由平行四边形的性质就可以得出结论；
（2）由（1）的结论建立方程求出x的值，就可以求出∠DCE的值，进而由平行线的性质求出∠D的度数．
（2）由（1）的结论建立方程求出x的值，就可以求出∠DCE的值，进而由平行线的性质求出∠D的度数．
解答：解：（1）∠A=∠DCE．
理由：∵AB∥CD，CE∥AD，
∴四边形AECD是平行四边形，
∴∠A=∠DCE；
（2）∵∠A=∠DCE，∠A=（3x-24）°，∠DCE=（56-x）°，
∴（3x-24）°=（56-x）°，
∴x=20°，
∴∠DCE=56°-20°=36°．
∵CE∥AD，
∴∠D+∠DCE=180°，
∴∠D=144°．
答：∠D的度数是144°．
理由：∵AB∥CD，CE∥AD，
∴四边形AECD是平行四边形，
∴∠A=∠DCE；
（2）∵∠A=∠DCE，∠A=（3x-24）°，∠DCE=（56-x）°，
∴（3x-24）°=（56-x）°，
∴x=20°，
∴∠DCE=56°-20°=36°．
∵CE∥AD，
∴∠D+∠DCE=180°，
∴∠D=144°．
答：∠D的度数是144°．
点评：本题考查了梯形的性质的运用，平行四边形的判定及性质的运用，解答时运用平行四边形的性质求解是关键．
练习册系列答案
阅读快车系列答案
相关题目
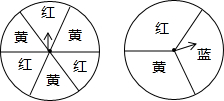如图，用两个转盘进行“配绿色”游戏（黄色和蓝色配在一起为绿色），同时转动两个转盘，当转盘停止转动时，用两盘指针所指的颜色配色，求能配出绿色的概率（用树形图或列表法表示）．
如图，在△ABC中，点D是AC上一点，添加下列哪个条件不能得到△CBD∽△CAB的是（ ）| A、∠CDB=∠CBA |
| B、∠CBD=∠A |
| C、BC•AB=BD•AC |
| D、BC2=CD•AC |
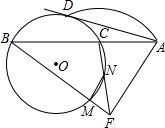已知：如图，AD切⊙O于点D，ACB为⊙O的割线，AP=AD，BP、CP分别交⊙O于M、N．求证：