题目内容
16.矩形的长与宽分别为a、b,下列数据能构成黄金矩形的是( )| A. | a=4,b=$\sqrt{5}$+2 | B. | a=4,b=$\sqrt{5}$-2 | C. | a=2,b=$\sqrt{5}$+1 | D. | a=2,b=$\sqrt{5}$-1 |
分析 根据黄金矩形的定义判断即可.
解答 解:∵宽与长的比是$\frac{\sqrt{5}-1}{2}$的矩形叫做黄金矩形,
∴$\frac{b}{a}$=$\frac{\sqrt{5}-1}{2}$,
∴a=2,b=$\sqrt{5}$-1,
故选D.
点评 本题主要考查了黄金矩形,记住定义是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
7.已知下列命题:
(1)16的平方根是±4
(2)若x=3,则x2-3x=0
(3)六边形的内角和是外角和的2倍
(4)顺次连接菱形四边中点的线段组成的四边形是矩形
其中原命题与逆命题均为真命题的个数是( )
(1)16的平方根是±4
(2)若x=3,则x2-3x=0
(3)六边形的内角和是外角和的2倍
(4)顺次连接菱形四边中点的线段组成的四边形是矩形
其中原命题与逆命题均为真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.YC市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够,导致出现需要租用却未租到车的现象,现将随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00-8:00需要租用公共自行车的人数是多少?
请回答下列问题:
| 时间 | 第一天7:00-8:00 | 第二天7:00-8:00 | 第三天7:00-8:00 | 第四天7:00-8:00 | 第五天7:00-8:00 |
| 需要租用自行车却未租到车的人数(人) | 1500 | 1200 | 1300 | 1300 | 1200 |
(2)由随机抽样估计,平均每天在7:00-8:00需要租用公共自行车的人数是多少?
5.分式方程$\frac{3}{x(x+1)}$=1-$\frac{3}{x+1}$的根为( )
| A. | -1或3 | B. | -1 | C. | 3 | D. | 1或-3 |
1.某班在一次数学测验后成绩统计如下表:
如果60分及以上为及格,那么这次数学测验的及格率是90%.
| 分数段(分) | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-100 |
| 人数 | 1 | 3 | 4 | 8 | 13 | 11 |
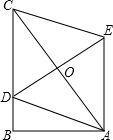 如图,在Rt△ABC中,∠B=90°,AB=5,BC=12,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是( )
如图,在Rt△ABC中,∠B=90°,AB=5,BC=12,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是( )