题目内容
16. 如图,点E是?ABCD中BC边延长线上一点,AE交CD于F,则图中的相似三角形有3对.
如图,点E是?ABCD中BC边延长线上一点,AE交CD于F,则图中的相似三角形有3对.
分析 先利用平行四边形的性质得AB∥CD,AD∥BC,根据平行于三角形的一边的直线与其它两边相交,所构成的三角形与原三角形相似,可分别判断△ADF∽ECF,△ECF∽△EBA,然后利用相似的传递性可得△EBA∽△ADF.
解答 解:∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∵AD∥CE,
∴△ADF∽ECF,
∵CF∥AB,
∴△ECF∽△EBA,
∴△EBA∽△ADF,
即图中的相似三角形有3对.
故答案为3对.
点评 本题考查了相似三角形的判定:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似.也考查了平行四边形的性质.

练习册系列答案
相关题目
6.在某小区花园中有x棵月季花,茶花的数量比月季花的棵数的3倍多7棵,则茶花的棵树是( )
| A. | 3x-7 | B. | 3x+7 | C. | 7x-3 | D. | 7x+3 |
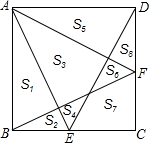 如图,正方形ABCD中,E,F分别是BC,CD边上的点,AE,DE,BF,AF把正方形分成8小块,试比较S3与S2+S7+S8的大小,并说明理由.
如图,正方形ABCD中,E,F分别是BC,CD边上的点,AE,DE,BF,AF把正方形分成8小块,试比较S3与S2+S7+S8的大小,并说明理由.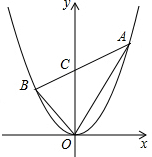 如图,过点C(0,3)的直线交抛物线y=x2于A、B两点,若S△AOB=6,求点A、B的坐标.
如图,过点C(0,3)的直线交抛物线y=x2于A、B两点,若S△AOB=6,求点A、B的坐标.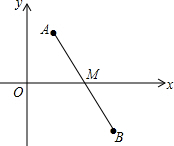 如图,在平面直角坐标系中存在两个点的坐标分别是A(1,2),B(3,-2).
如图,在平面直角坐标系中存在两个点的坐标分别是A(1,2),B(3,-2). 如图是由六块积木搭成,这几块积木都是相同的正方体,请画出这个图形的三视图:
如图是由六块积木搭成,这几块积木都是相同的正方体,请画出这个图形的三视图: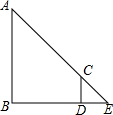 古塔测高有一座古塔,不知有多高,测得影长为11.3米,现将一长为0.8米的竹竿直立,使其影子的末端与塔影的末端重合,测得竹竿的影长为0.2米,求塔高.
古塔测高有一座古塔,不知有多高,测得影长为11.3米,现将一长为0.8米的竹竿直立,使其影子的末端与塔影的末端重合,测得竹竿的影长为0.2米,求塔高. 小刚要从A地赶往C地去参加科技夏令营,他拿出一张地图,图上有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A的南偏西55°,在B地的北偏西70°,如图所示.
小刚要从A地赶往C地去参加科技夏令营,他拿出一张地图,图上有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A的南偏西55°,在B地的北偏西70°,如图所示.