题目内容
3.计算:$\sqrt{18}$-$\sqrt{2}$=( )| A. | 3 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
分析 先把各根式化为最简二次根式,再合并同类项即可.
解答 解:原式=3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$.
故选C.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
相关题目
12.下列二次根式中的最简二次根式是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{1.2}$ | C. | $\sqrt{10}$ | D. | $\sqrt{\frac{1}{3}}$ |
13.下列结论正确的是( )
| A. | $\frac{1}{4}$的算术平方根是$\frac{1}{2}$ | B. | -2没有立方根 | ||
| C. | 4的算术平方根是±2 | D. | 立方根等于本身的数只有0 |
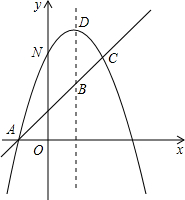 如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N.其顶点为D.