Question

【题目】如图，已知一次函数的图象与反比例函数的图象交于点，与轴、轴交于两点，过作垂直于轴于点.已知.

（1）求一次函数和反比例函数的表达式；

（2）观察图象:当时，比较.

Answer 1

【答案】（1）;（2）

【解析】

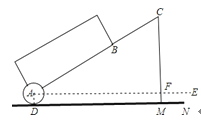
（1）由一次函数的解析式可得出D点坐标，从而得出OD长度，再由△ODC与△BAC相似及AB与BC的长度得出C、B、A的坐标，进而算出一次函数与反比例函数的解析式；
（2）以A点为分界点，直接观察函数图象的高低即可知道答案．

解：（1）对于一次函数y=kx-2，令x=0，则y=-2，即D（0，-2），
∴OD=2，
∵AB⊥x轴于B，
∴ ，
∵AB=1，BC=2，
∴OC=4，OB=6，
∴C（4，0），A（6，1）
将C点坐标代入y=kx-2得4k-2=0，
∴k=，
∴一次函数解析式为y=x-2；
将A点坐标代入反比例函数解析式得m=6，
∴反比例函数解析式为y=；
（2）由函数图象可知：
当0＜x＜6时，y1＜y2；
当x=6时，y1=y2；
当x＞6时，y1＞y2；