题目内容
9.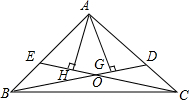 已知,如图,在△ABC中,AB=AC,BD与CE相交于O,AH⊥CE,H为垂足,AG⊥BD,G为垂足,AH=AG.求证:AD=AE.
已知,如图,在△ABC中,AB=AC,BD与CE相交于O,AH⊥CE,H为垂足,AG⊥BD,G为垂足,AH=AG.求证:AD=AE.
分析 由条件可先证明△ABG≌△ACH,可得∠BAG=∠CAH,利用角的和差可证得∠EAH=∠DAG,可证明△AEH≌△ADG,可证得AD=AE.
解答 证明:
∵AH⊥CE,AG⊥BD,
∴∠AGB=∠AHC=90°,
在Rt△ABG和Rt△ACH中
$\left\{\begin{array}{l}{AB=AC}\\{AH=AG}\end{array}\right.$
∴Rt△ABG≌RtACH(HL),
∴∠BAG=∠CAH,
∴∠EAH=∠DAG,
在△AEH和△ADG中
$\left\{\begin{array}{l}{∠EAH=∠DAG}\\{AH=AG}\\{∠AHE=∠AGD}\end{array}\right.$
∴△AEH≌△ADG(ASA),
∴AD=AE.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
相关题目
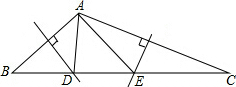 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.若BC=10,则△ADE周长是多少?为什么?
如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.若BC=10,则△ADE周长是多少?为什么?