题目内容
6. 如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明△ADC∽△CDB.
如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明△ADC∽△CDB.
分析 根据三角形内角和定理和已知求出∠B=∠ACD,根据相似三角形的判定得出△ADC∽△CDB,根据相似三角形的性质得出比例式,即可得出结论.
解答 解:△ADC∽△CBD,
理由是:∵在Rt△ABC中,∠C=90°.CD是斜边AB上的高,
∴∠ACB=∠CDB=∠CDA=90°,
∴∠B+∠BCD=90°,∠BCD+∠ACD=90°,
∴∠B=∠ACD,
∵∠CDB=∠ADC=90°,
∴△ADC∽△CDB,
∴$\frac{CD}{BD}$=$\frac{AD}{CD}$,
∴CD2=BD•AD,
故答案为△ADC,△CDB.
点评 本题考查了相似三角形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
14.如果a+b=2,那么a2+2ab+b2的值是( )
| A. | 2 | B. | 4 | C. | -2 | D. | -4 |
18.“神舟六号”宇航员费俊龙、聂海胜在太空共看到了76次日出日落,日行程约676000公里,用科学记数法表示日行程为( )
| A. | 6.76×107公里 | B. | 6.76×105公里 | C. | 0.676×106公里 | D. | 67.6×106公里 |
15.下列计算中,正确的是( )
| A. | a2+a3=a5 | B. | a2•a3=a6 | C. | a9÷a3=a3 | D. | (-a3)2=a6 |
16.下列事件为必然事件的有( )个
①过三点可以确定一个圆 ②平分弦的直径必垂直这条弦
③一个数的零次幂为零 ④两点确定一条直线.
①过三点可以确定一个圆 ②平分弦的直径必垂直这条弦
③一个数的零次幂为零 ④两点确定一条直线.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
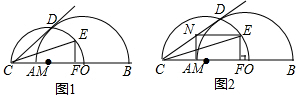
 如图所示,点B在点A南偏东39°方向.
如图所示,点B在点A南偏东39°方向.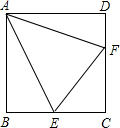 如图,点E,F分别为正方形ABCD的边BC、CD上一点,且AE平分∠BEF,连AF.
如图,点E,F分别为正方形ABCD的边BC、CD上一点,且AE平分∠BEF,连AF.