题目内容
1．已知点A（a，0）和点B（0，4）两点，且直线AB与坐标轴围成的三角形的面积等于8，则a的值是2或-2．分析 先分别表示出OA=|a|，OB=4，然后根据三角形面积公式得到$\frac{1}{2}$•|a|•4=4，然后解绝对值方程即可．
解答 解：根据题意得$\frac{1}{2}$OA•OB=8，
即$\frac{1}{2}$•|a|•4=4，
解得a=2或-2．
故答案为2或-2．
点评 本题考查了坐标与图形性质：利用平行于坐标的直线上点的坐标特征计算相应线段的长．解决本题的关键是利用坐标计算线段的长．
练习册系列答案
名校课堂系列答案
相关题目
12．
如图，已知：∠MON=30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=1，则△A5B5A6的边长为（ ）
如图，已知：∠MON=30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=1，则△A5B5A6的边长为（ ）| A． | 6 | B． | 16 | C． | 32 | D． | 64 |
9．反比例函数y=$\frac{k}{x}$的自变量x满足2≤x≤4，函数值y满足$\frac{1}{2}$≤y≤1，则这个反比例函数为（ ）
| A． | y=$\frac{1}{x}$ | B． | y=$\frac{2}{x}$ | C． | y=$\frac{4}{x}$ | D． | y=$\frac{1}{2x}$ |
16．对于函数y=-$\frac{5}{x}$，下列说法错误的是（ ）
| A． | 它的图象分布在二、四象限 | |
| B． | 它的图象既是轴对称图形又是中心对称图形 | |
| C． | 当x＞0时，y的值随x的增大而增大 | |
| D． | 当x＜0时，y的值随x的增大而减小 |
10．在△ABC中，∠BAC=90°，AB=3，AC=4，D是BC的中点，则BD的长为（ ）
| A． | 5 | B． | $\frac{5}{2}$ | C． | 2 | D． | $\frac{3}{2}$ |
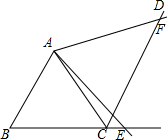已知，如图，△ABC为等边三角形，CD∥AB，点E、F分别在BC延长线及CD上，∠EAF=60°，求证：BE=CF．