题目内容
15. 如图,AD是△ABC的高,BE是△ABC的内角平分线,BE、AD相交于点F,已知∠BAD=40°,则∠BFD=65°.
如图,AD是△ABC的高,BE是△ABC的内角平分线,BE、AD相交于点F,已知∠BAD=40°,则∠BFD=65°.
分析 根据高线的定义可得∠ADB=90°,然后根据∠BAD=40°,求出∠ABC的度数,再根据角平分线的定义求出∠FBD,然后利用三角形的内角和等于180°列式计算即可得解.
解答 解:∵AD是高线,
∴∠ADB=90°
∵∠BAD=40°,
∴∠ABC=50°,
∵BE是角平分线,
∴∠FBD=25°,
在△FBD中,∠BFD=180°-90°-25°=65°.
故答案为:65°.
点评 本题考查了三角形的内角和定理,角平分线的定义,高线的定义,熟记概念与定理并准确识图是解题的关键.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
6.若x>y,则下列式子中错误的是( )
| A. | x+$\frac{1}{3}$>y+$\frac{1}{3}$ | B. | x-3>y-3 | C. | $\frac{x}{3}$>$\frac{y}{3}$ | D. | -3x>-3y |
20.将(2-x)$\sqrt{\frac{1}{x-2}}$根号外的因式移到根号内,得( )
| A. | $\sqrt{x-2}$ | B. | $\sqrt{2-x}$ | C. | -2$\sqrt{2-x}$ | D. | -$\sqrt{x-2}$ |
7.镇江市教育局为帮助全市贫困师生举行“一日捐”活动,甲、乙两校教师各捐款60000元,已知“…”,设乙学校教师有x人,则可得方程$\frac{60000}{x}$-$\frac{60000}{(1+20%)x}$=20,根据此情景,题中用“…”表示的缺失的条件应补( )
| A. | 乙校教师比甲校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20% | |
| B. | 甲校教师比乙校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20% | |
| C. | 甲校教师比乙校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20% | |
| D. | 乙校教师比甲校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20% |
5.下列说法中正确的是( )
| A. | 已知a,b,c是三角形的三边长,则a2+b2=c2 | |
| B. | 在直角三角形中,两边长和的平方等于第三边长的平方 | |
| C. | 在Rt△ABC中,若∠C=90°,则三角形对应的三边满足a2+b2=c2 | |
| D. | 在Rt△ABC中,若∠A=90°,则三角形对应的三边满足a2+b2=c2 |
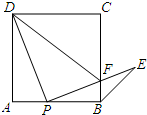 如图,点P是正方形ABCD边AB上一点(不与点A.B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F.连接BE、DF.
如图,点P是正方形ABCD边AB上一点(不与点A.B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F.连接BE、DF.