题目内容
 某一时刻,树AB在阳光下的影子一部分在地面上,另一部分在建筑物的墙面上.设树AB在地面上的影长BC为5.2m,墙面上的影长CD为1.5m;同一时刻测得竖立于地面长1m的木杆的影长为0.8m,求树高.
某一时刻,树AB在阳光下的影子一部分在地面上,另一部分在建筑物的墙面上.设树AB在地面上的影长BC为5.2m,墙面上的影长CD为1.5m;同一时刻测得竖立于地面长1m的木杆的影长为0.8m,求树高.考点:相似三角形的应用,平行投影
专题:
分析:此题是实际应用问题,解题的关键是将实际问题转化为数学问题解答;根据在同一时刻物高与影长成正比例.利用相似三角形的对应边成比例解答即可.
解答: 解:过点D作DE⊥AB于点E,
解:过点D作DE⊥AB于点E,
∵AB⊥BC,DC⊥BC,
∴四边形BCDE是矩形,
∴BC=DE=5.2m,BE=CD=1.5m,
∵在同一时刻物高与影长成正比,
∴
=
,即
=
,解得
∴AE=6.5m,
∴AB=AE+EB=6.5+1.5=8m,
∴树的高度为8m.
答:树的高度为8m.
 解:过点D作DE⊥AB于点E,
解:过点D作DE⊥AB于点E,∵AB⊥BC,DC⊥BC,
∴四边形BCDE是矩形,
∴BC=DE=5.2m,BE=CD=1.5m,
∵在同一时刻物高与影长成正比,
∴
| AE |
| DE |
| 1 |
| 0.8 |
| AE |
| 5.2 |
| 1 |
| 0.8 |
∴AE=6.5m,
∴AB=AE+EB=6.5+1.5=8m,
∴树的高度为8m.
答:树的高度为8m.
点评:本题考查的是相似三角形的应用,熟知在同一时刻物高与影长成正比是解答此题的关键.

练习册系列答案
相关题目
下列去括号正确的是( )
| A、-(2x-1)=-2x-1 |
| B、-(2x-1)=-2x+1 |
| C、2(x-1)=2x-1 |
| D、-3(x+1)=-3x+3 |
若a=(-
)+(-
)-(-
),则a的相反数为( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
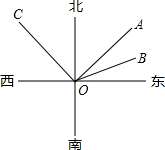 如图所示,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A、B、C处时,经测量得,甲船位于港口的北偏东44°方向,乙船位于港口的北偏东76°方向,丙船位于港口的北偏西45°方向.
如图所示,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A、B、C处时,经测量得,甲船位于港口的北偏东44°方向,乙船位于港口的北偏东76°方向,丙船位于港口的北偏西45°方向. 如图,已知∠A=42°,求劣弧AB的度数.
如图,已知∠A=42°,求劣弧AB的度数. 如图,在⊙O中,弦AB与CD相交于点F,∠BCD=40°,∠BFD=70°,求∠ADC的度数.
如图,在⊙O中,弦AB与CD相交于点F,∠BCD=40°,∠BFD=70°,求∠ADC的度数.