题目内容
5．在Rt△ABC中，∠C=90°，证明：sinA=cosB．分析 根据锐角三角函数的定义得出sinA=$\frac{BC}{AB}$，cosB=$\frac{BC}{AB}$，等量代换即可证明sinA=cosB．
解答 
证明：如图．
∵在Rt△ABC中，∠C=90°，
∴sinA=$\frac{BC}{AB}$，cosB=$\frac{BC}{AB}$，
∴sinA=cosB．
点评 本题考查锐角三角函数的定义：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．
练习册系列答案
计算高手系列答案
相关题目
15．下列运用等式的性质变形不正确的是（ ）
| A． | 若a-b=0，则a=b | B． | 若-$\frac{1}{2}$x=-4，则x=2 | ||
| C． | 若a=b，则2a-5=2b-5 | D． | 若a=b，则$\frac{a}{-4}$=$\frac{b}{-4}$ |
16．下列各题中的变形，属于移项的是（ ）
| A． | 由2x-2y-1得-1-2y+2x | B． | 由6x-1=x+5得6x-1=5+x | ||
| C． | 由4-x=3x-2得3x-2=4-x | D． | 由2-x=x-2得2+2=x+x |
13．学校举行排球赛，积分榜部分情况如下．
（1）分析积分榜，平一场比负一场多得1分．
（2）若胜一场得3分，七（6）班也比赛了6场，胜场是平场的一半且共积14分，那么七（6）班胜几场？
| 班级 | 比赛场次 | 胜场 | 平场 | 负场 | 积分 |
| 七（1）班 | 6 | 3 | 2 | 1 | 14 |
| 七（2）班 | 6 | 1 | 4 | 1 | 12 |
| 七（3）班 | 6 | 5 | 0 | 1 | 16 |
| 七（4）班 | 6 | 5 | 1 | 0 | 17 |
（2）若胜一场得3分，七（6）班也比赛了6场，胜场是平场的一半且共积14分，那么七（6）班胜几场？
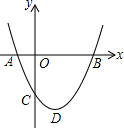如图，二次函数y=ax2+bx+c（a＞0）图象的顶点为D，其图象与x轴的交点A、B的横坐标分别为-1，3．与y轴负半轴交于点C，在下面五个结论中：