题目内容
17.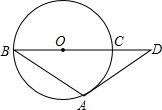 已知,BC是圆O的直径,AB是圆O的弦,过点A的切线交BC延长线于点D,若AB=AD=2$\sqrt{3}$,则弧AC的长为$\frac{2}{3}π$.
已知,BC是圆O的直径,AB是圆O的弦,过点A的切线交BC延长线于点D,若AB=AD=2$\sqrt{3}$,则弧AC的长为$\frac{2}{3}π$.
分析 连接OA,由AD是⊙O的切线,得到∠OAD=90°,于是得到∠D+∠AOC=90°,根据等腰三角形的性质和直角三角形的性质得到∠AOC=60°,求得AO=$\frac{\sqrt{3}}{3}$AD=2,于是结论即可得出.
解答 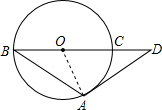 解:连接OA,
解:连接OA,
∵AD是⊙O的切线,
∴∠OAD=90°,
∴∠D+∠AOC=90°,
∵AB=AD=2$\sqrt{3}$,
∴∠B=∠D,
∵OA=OB,
∴∠B=∠OAB,
∴∠AOC=2∠B=2∠D,
∴∠AOC=60°,
∴AO=$\frac{\sqrt{3}}{3}$AD=2,
∴弧AC的长=$\frac{60π×2}{180}$=$\frac{2}{3}π$,
故答案为:$\frac{2}{3}π$.
点评 本题考查了切线的性质,等腰三角形的性质,三角函数,结论OA构造直角三角形是解题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
8.矩形的长是宽的2倍,对角线的长是5cm,则这个矩形的长是( )
| A. | $\frac{5}{2}$cm | B. | $\sqrt{5}$cm | C. | 2$\sqrt{5}$cm | D. | $\frac{\sqrt{5}}{2}$cm |
12.今年植树节,学校团委组织60位团员去植树,他们共种了130棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人,根据题意,列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=130}\\{3x+2y=60}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=130}\\{2x+3y=60}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=60}\\{3x+2y=130}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=60}\\{2x+3y=130}\end{array}\right.$ |
7.在Rt△ABC中,AB=3,AC=4,则BC的长为( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 无法确定 |
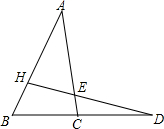 如图,下列结论:①∠A>∠ACD;②∠AED>∠B+∠D;③∠B+∠ACB<180°;④∠HEC>∠B.其中正确的是②③④(填上你认为正确的所有序号).
如图,下列结论:①∠A>∠ACD;②∠AED>∠B+∠D;③∠B+∠ACB<180°;④∠HEC>∠B.其中正确的是②③④(填上你认为正确的所有序号).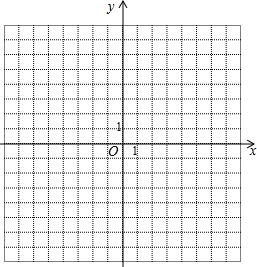 如图,在平面直角坐标系中,某四边形的四个顶点的坐标分别为:A(4,-2),B(6,2),C(4,6),D(2,2).
如图,在平面直角坐标系中,某四边形的四个顶点的坐标分别为:A(4,-2),B(6,2),C(4,6),D(2,2).