题目内容
9.当x为何值时,代数式-$\frac{1}{6}$x+3的值比6x-3的值大.分析 先根据题意得出关于x的不等式,再去分母,再去括号,移项,合并同类项,把x的系数化为1即可.
解答 解:由题意得,-$\frac{1}{6}$x+3>6x-3,
去分母得,-x+18>6(6x-3),
去括号得,-x+18>36x-18,
移项得,-x-36x>-18-18,
合并同类项,-37x>-36,
把x的系数化为1得,x<$\frac{36}{37}$.
因此,当<$\frac{36}{37}$时,代数式-$\frac{1}{6}$x+3的值比6x-3的值大.
点评 本题考查的是解一元一次不等式,熟知解一元一次不等式得基本步骤是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.下列从左到右的变形是因式分解的是( )
| A. | (x+1)(x-1)=x2-1 | B. | (a-3)(a+7)=a2+4a-21 | ||
| C. | x2+x+$\frac{1}{4}$=(x+$\frac{1}{2}$)2 | D. | 3x3-6x2+4=3x2(x-2)+4 |
1.下列各组数中,以它们为边长的线段不能构成直角三角形的是( )
| A. | 2,2,3 | B. | 3,4,5 | C. | 5,12,13 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
18.已知y=(m-3)x|m|-2+1是一次函数,则m的值是( )
| A. | -3 | B. | 3 | C. | ±3 | D. | ±2 |
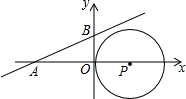 如图,直线y=$\frac{{\sqrt{3}}}{3}$x+$\sqrt{3}$与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
如图,直线y=$\frac{{\sqrt{3}}}{3}$x+$\sqrt{3}$与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )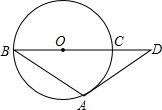 已知,BC是圆O的直径,AB是圆O的弦,过点A的切线交BC延长线于点D,若AB=AD=2$\sqrt{3}$,则弧AC的长为$\frac{2}{3}π$.
已知,BC是圆O的直径,AB是圆O的弦,过点A的切线交BC延长线于点D,若AB=AD=2$\sqrt{3}$,则弧AC的长为$\frac{2}{3}π$.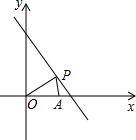 已知直线l为x+y=8,点P(x,y)在l上,且x>0,y>0,点A的坐标为(6,0).
已知直线l为x+y=8,点P(x,y)在l上,且x>0,y>0,点A的坐标为(6,0).