Question

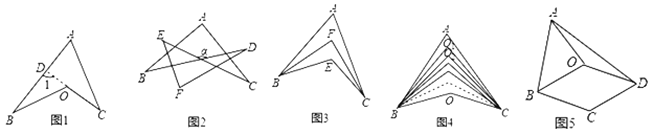
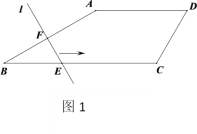
【题目】图1是某酒店的推拉门，已知门的宽度AD=2米，两扇门的大小相同（即AB=CD)，且AB+CD=AD，现将右边的门CDD1C1绕门轴DD1向外面旋转67°（如图2所示）．

参考数据：(sin67°≈0.92，cos67°≈0.39，tan29.6°≈0．57,tan19.6°≈0.36，sin29.6°≈0.49）

（1）求点C到直线AD的距离．

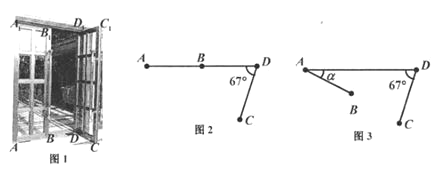
（2）将左边的门ABB1A1绕门轴AA1向外面旋转，设旋转角为a（如图3所示），问当a为多少度时，点B，C之间的距离最短．

Answer 1

【答案】（1）点C到直线AD的距离为0.92米；（2）当旋转角为a为29.6°时，点B，C之间的距离最短.

【解析】

利用三角函数的应用（1）作CE⊥AD交AD于点E,根据，求出CE的值，即C点到AD的距离.（2）要使点B，C之间的距离最短，只需满足AB所在的直线经过点C．由(1)可知CE的长利用cos67°求出DE的长，然后算出AE，根据tanA= ，求出∠A的度数.

（1）解： 作CE⊥AD交AD于点E．

∴sin 67°=

即CE=CD sin 67°=1×0.92=0.92．

∴点C到直线AD的距离为0.92米．

（2）解：要使点B，C之间的距离最短，只需满足AB所在的直线经过点C．（如图3）

由（1）知CE=0.92，DE=CD cos67°=1×0.39=0.39．

∴AE=2-0.39=1.61．

∴在Rt△AEC中，tanA= =≈0.57．

∴∠A=29.6°．

即当旋转角为a为29.6°时，点B，C之间的距离最短.