题目内容
4.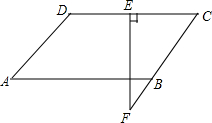 如图,在?ABCD中,∠ABC=3∠A,点E在CD上,且CE=4,EF⊥CD交CB的延长线于点F,求CF的长.
如图,在?ABCD中,∠ABC=3∠A,点E在CD上,且CE=4,EF⊥CD交CB的延长线于点F,求CF的长.
分析 利用平行四边形的性质得出∠A=x,则∠ABC=3x,故x+3x=180°,进而得出∠C=45°,再利用勾股定理求出FC的长.
解答 解:∵在?ABCD中,∠ABC=3∠A,
∴设∠A=x,则∠ABC=3x,
故x+3x=180°,
解得:x=45°,
则∠C=45°,
∵CE=4,EF⊥CD,
∴EF=4,
∴FC=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
点评 此题主要考查了平行四边形的性质以及勾股定理得出EF=EC是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目