题目内容
已知二次函数y=x2+kx+2与x轴两个交点A、B都在原点左侧,顶点为C,当△ABC为等腰直角三角形时,求k的值.
考点:抛物线与x轴的交点
专题:
分析:根据条件画出大致图象,作CD⊥AB于D,可以得出二次函数的顶点坐标为(-
,
),CD=|
|=
AB,设A(x1,0),B(x2,0),就有AB=|x2-x1|,就可以建立方程|
|=
|x2-x1|,由根与系数的关系就可以得出x1+x2=-k,x1x2=2,将方程变形后求出其解即可.
| k |
| 2 |
| 8-k2 |
| 4 |
| 8-k2 |
| 4 |
| 1 |
| 2 |
| 8-k2 |
| 4 |
| 1 |
| 2 |
解答:解:如图,设A(x1,0),B(x2,0),作CD⊥AB于D,
∴AB=|x2-x1|,
∵△ABC为等腰直角三角形,
∴CD=
AB.
∵y=x2+kx+2,
∴y=(x+
)2+
,
∴C(-
,
),
∴CD=|
|,
∴|
|=
|x2-x1|,
(
)2=[
(x2-x1]2,
=
[(x2+x1)2-4x1x2],
∵x1+x2=-k,x1x2=2,
∴
=
(k2-8),
k4-20k2+96=0,
解得:k1=2
,k2=-2
,k3=2
,k4=-2
.
∵抛物线与x轴两个交点A、B都在原点左侧,
∴a、b同号,
∵a=1>0,
∴b=k>0
∴k=2
或2
,
∵k=2
时,b2-4ac=0,
∴抛物线与x轴只有一个交点,
∴k=2
.
答:k的值为2
.
∴AB=|x2-x1|,
∵△ABC为等腰直角三角形,

∴CD=
| 1 |
| 2 |
∵y=x2+kx+2,
∴y=(x+
| k |
| 2 |
| 8-k2 |
| 4 |
∴C(-
| k |
| 2 |
| 8-k2 |
| 4 |
∴CD=|
| 8-k2 |
| 4 |
∴|
| 8-k2 |
| 4 |
| 1 |
| 2 |
(
| 8-k2 |
| 4 |
| 1 |
| 2 |
| 64-16k2+k4 |
| 16 |
| 1 |
| 4 |
∵x1+x2=-k,x1x2=2,
∴
| 64-16k2+k4 |
| 16 |
| 1 |
| 4 |
k4-20k2+96=0,
解得:k1=2
| 2 |
| 2 |
| 3 |
| 3 |
∵抛物线与x轴两个交点A、B都在原点左侧,
∴a、b同号,
∵a=1>0,
∴b=k>0
∴k=2
| 2 |
| 3 |
∵k=2
| 2 |
∴抛物线与x轴只有一个交点,
∴k=2
| 3 |
答:k的值为2
| 3 |
点评:本题考查了抛物线的顶点式的运用,等腰直角三角形的性质的运用,根与系数的关系的运用,高次方程的解法的运用,解答时运用抛物线的性质求解是关键.

练习册系列答案
相关题目
下面各式中,计算正确的是( )
| A、-22=4 | |||
B、
| |||
C、
| |||
| D、(-1)3=-3 |
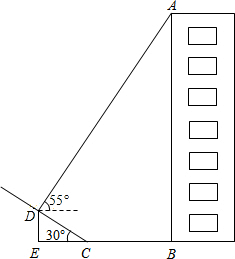 如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=4m.在D点处观察点A的仰角为55°,已知坡角为30°,你能求出楼房AB的高度吗?(sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,结果精确到0.1m)
如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=4m.在D点处观察点A的仰角为55°,已知坡角为30°,你能求出楼房AB的高度吗?(sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,结果精确到0.1m)