题目内容
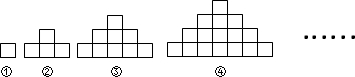
(1)如图,第n个图形中小正方形的个数是 ;
(2)求1+3= ,1+3+5= ,1+3+5+7= ,1+3+5+7+9= ,1+3+5+7+9+…+(2n-1)= .
(2)求1+3=

考点:规律型:图形的变化类,规律型:数字的变化类
专题:
分析:(1)由图可知:第一个图形有1个正方形;第二个图形有1+3=4=22个正方形;第三个图形有1+3+5=9=32个正方形,…由此得出第n个图形中小正方形的个数是1+3+5+7+9+…+(2n-1)=n2;
(2)由(1)的方法直接得出结果即可.
(2)由(1)的方法直接得出结果即可.
解答:解:(1)第一个图形有1个正方形;
第二个图形有1+3=4=22个正方形;
第三个图形有1+3+5=9=32个正方形,
…
所以第n个图形中小正方形的个数是1+3+5+7+9+…+(2n-1)=n2
(2)求1+3=22,1+3+5=32,1+3+5+7=42,1+3+5+7+9=52,1+3+5+7+9+…+(2n-1)=n2.
故答案为:n2;22,32,42,52,n2.
第二个图形有1+3=4=22个正方形;
第三个图形有1+3+5=9=32个正方形,
…
所以第n个图形中小正方形的个数是1+3+5+7+9+…+(2n-1)=n2
(2)求1+3=22,1+3+5=32,1+3+5+7=42,1+3+5+7+9=52,1+3+5+7+9+…+(2n-1)=n2.
故答案为:n2;22,32,42,52,n2.
点评:此题考查数字的变化规律和图形的变化规律,找出数字与图形之间的联系,得出规律,解决问题.

练习册系列答案
相关题目
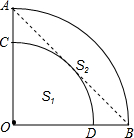 如图,∠AOB=90°,
如图,∠AOB=90°, |
| AB |
 |
| CD |
 |
| CD |
| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、不确定 |
 甲、乙两人同时从相距180千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留1小时后返回A地.如图是他们离A地的距离y(千米)与时间x(时)之间的函数关系图象.
甲、乙两人同时从相距180千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留1小时后返回A地.如图是他们离A地的距离y(千米)与时间x(时)之间的函数关系图象.