题目内容
在平面直角坐标系中,A(a,0),B(0,b)满足(a-2)2+
=0.
(1)求直线AB的解析式;
(2)若点M为直线y=mx上一点,△ABM是以AB为底的等腰直角三角形,求m的值.
| b-4 |
(1)求直线AB的解析式;
(2)若点M为直线y=mx上一点,△ABM是以AB为底的等腰直角三角形,求m的值.
考点:一次函数综合题
专题:
分析:(1)根据非负数的性质可求得a、b,可求得A、B坐标,利用待定系数法可求得直线AB的解析式;
(2)根据A、B坐标,可求出AB及AB中点的C坐标,设M坐标为(x,mx),则MC=
AB,且M点在线段AB的垂直平分线上,可求得垂直平分线的方程,则可求得M的值.
(2)根据A、B坐标,可求出AB及AB中点的C坐标,设M坐标为(x,mx),则MC=
| 1 |
| 2 |
解答:解:
(1)∵(a-2)2+
=0,
∴a=2,b=4,
∴A(2,0),B(0,4),
设直线AB解析式为y=kx+b,把A、B两点坐标代入可得
,
解得
,
∴直线AB的解析式为y=-2x+4;
(2)∵A(2,0),B(0,4),
∴线段AB的中点C为(1,2),AB=2
,
∵直线AB解析式为y=-2x+4,
∴可设线段AB垂直平分线的解析式为y=
x+m,
把C点坐标代入可得b=
,
∴线段AB的垂直平分线为y=
x+
,
当△ABM是以AB为底的等腰直角三角形时,可知MC=
AB=
,
∵M在直线y=mx上,
∴设M坐标为(x,mx),
∴MC=
=
,
又M在线段AB的垂直平分线上,
∴mx=
x+
,
代入上式,整理可得(x-1)2=4,
解得x=3或x=-1,
当x=3时,y=
×3+
=3,此时点M坐标为(3,3),代入y=mx可求得m=1,
当x=-1时,y=
×(-1)+
=1,此时点M坐标为(-1,1),代入y=mx可求得m=-1,
综上可知m为1或-1.
(1)∵(a-2)2+
| b-4 |
∴a=2,b=4,
∴A(2,0),B(0,4),
设直线AB解析式为y=kx+b,把A、B两点坐标代入可得
|
解得
|
∴直线AB的解析式为y=-2x+4;
(2)∵A(2,0),B(0,4),
∴线段AB的中点C为(1,2),AB=2
| 5 |
∵直线AB解析式为y=-2x+4,
∴可设线段AB垂直平分线的解析式为y=
| 1 |
| 2 |
把C点坐标代入可得b=
| 3 |
| 2 |
∴线段AB的垂直平分线为y=
| 1 |
| 2 |
| 3 |
| 2 |
当△ABM是以AB为底的等腰直角三角形时,可知MC=
| 1 |
| 2 |
| 5 |
∵M在直线y=mx上,
∴设M坐标为(x,mx),
∴MC=
| (x-1)2+(mx-2)2 |
| 5 |
又M在线段AB的垂直平分线上,
∴mx=
| 1 |
| 2 |
| 3 |
| 2 |
代入上式,整理可得(x-1)2=4,
解得x=3或x=-1,
当x=3时,y=
| 1 |
| 2 |
| 3 |
| 2 |
当x=-1时,y=
| 1 |
| 2 |
| 3 |
| 2 |
综上可知m为1或-1.
点评:本题主要考查待定系数法求函数解析式和等腰直角三角形的性质、垂直平分线的方程、直线的交点等知识的综合应用.在(1)中掌握非负数的性质是解题的关键,在(2)中确定出M点所在的直线是解题的关键.注意方程思想和勾股定理的应用,难度适中,综合性较强.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
已知⊙O的半径为3,线段OP的长度为2,则点P与⊙O的位置关系是( )
| A、点P在⊙O内 |
| B、点P在⊙O上 |
| C、点P在⊙O外 |
| D、无法确定 |
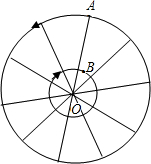 如图,一个同心圆圈的玩具,内外都等分成10格,都可绕着O点转动,若内圈按顺时针方向旋转,外圈按逆时针方向旋转,且内圈旋转的速度是外圈的4倍,当射线OB、OA按规定的方向同时转动:
如图,一个同心圆圈的玩具,内外都等分成10格,都可绕着O点转动,若内圈按顺时针方向旋转,外圈按逆时针方向旋转,且内圈旋转的速度是外圈的4倍,当射线OB、OA按规定的方向同时转动: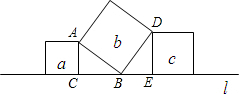 如图,直线l上有三个正方形a、b、c,其中a、c的面积分别为5和11.求正方形b的面积.
如图,直线l上有三个正方形a、b、c,其中a、c的面积分别为5和11.求正方形b的面积. 如图,反比例函数y=
如图,反比例函数y=