题目内容
6. 如图,AB为⊙O的直径,AC为⊙O的弦,AD平分∠BAC,交⊙O于点D,DE⊥C,交AC的延长线于点E.
如图,AB为⊙O的直径,AC为⊙O的弦,AD平分∠BAC,交⊙O于点D,DE⊥C,交AC的延长线于点E.(1)求证:直线DE是⊙O的切线;
(1)若AE=8,⊙O的半径为5,求DE的长.
分析 (1)连接OD,由角平分线和等腰三角形的性质得出∠ODA=EAD,证出EA∥OD,再由已知条件得出DE⊥OD,即可得出结论.
(2)作DF⊥AB,垂足为F,由AAS证明△EAD≌△FAD,得出AF=AE=8,DF=DE,求出OF=3,由勾股定理得出DF,即可得出结果.
解答 (1)证明: 连接OD,如图1所示:
连接OD,如图1所示:
∵AD平分∠BAC,
∴∠EAD=∠OAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠ODA=EAD,
∴EA∥OD,
∵DE⊥EA,
∴DE⊥OD,
∵点D在⊙O上,
∴直线DE与⊙O相切.
(2)解:作DF⊥AB,垂足为F,如图2所示:
∴∠DFA=∠DEA=90°,
在△EAD和△FAD中,
$\left\{\begin{array}{l}{∠DFA=∠DEA}\\{∠EAD=∠FAD}\\{AD=AD}\end{array}\right.$,
∴△EAD≌△FAD(AAS),
∴AF=AE=8,DF=DE,
∵OA=OD=5,
∴OF=3,
在Rt△DOF中,DF=$\sqrt{O{D}^{2}-O{F}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴DE=DF=4.
点评 本题考查圆与直线相切的判定、平行线的判定与性质、三角形全等的判定与性质、勾股定理等知识,熟练掌握切线的判定方法,证明三角形全等是解决问题(2)的关键.

练习册系列答案
相关题目
16.下列各式,计算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | 3$\sqrt{3}-\sqrt{3}$=3 | C. | 2$\sqrt{5}×3\sqrt{5}=6\sqrt{5}$ | D. | ($\sqrt{8}-\sqrt{6}$)÷$\sqrt{2}$=2-$\sqrt{3}$ |
11.下列各式由左边到右边的变形,是因式分解的是( )
| A. | (a+1)(a-1)=a2-1 | B. | (x-y)(m-n)=(y-x)(n-m) | C. | ab-a-b+1=(a-1)(b-1) | D. | m2-2m-3=m(m-2)-3 |
18.估算$\sqrt{26}$-2的值( )
| A. | 在1到2之间 | B. | 在2到3之间 | C. | 在3到4之间 | D. | 在4到5之间 |
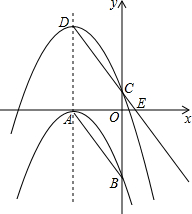 如图,抛物线C1:y=-$\frac{4}{9}$(x+3)2与x,y轴分别相交于点A,B,将抛物线C1沿对称轴向上平移,记平移后的抛物线为C2,抛物线C2的顶点是D,与y轴交于点C,射线DC与x轴相交于点E,
如图,抛物线C1:y=-$\frac{4}{9}$(x+3)2与x,y轴分别相交于点A,B,将抛物线C1沿对称轴向上平移,记平移后的抛物线为C2,抛物线C2的顶点是D,与y轴交于点C,射线DC与x轴相交于点E, 如图,己知点B,D在AC的两侧,E,F分别是△ACD与△ABC的重心,且EF=2,则BD的长度是( )
如图,己知点B,D在AC的两侧,E,F分别是△ACD与△ABC的重心,且EF=2,则BD的长度是( )