��Ŀ����
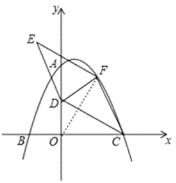
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ���������ύ��A��B��C���㣬���е�A������Ϊ��0��8������B������Ϊ����4��0��.
��ͼ���������ύ��A��B��C���㣬���е�A������Ϊ��0��8������B������Ϊ����4��0��.
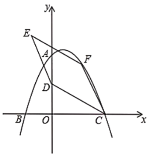
��1����ö��κ����ı���ʽ����C�����ꣻ
��2����D������Ϊ��0��4������FΪ�ö��κ����ڵ�һ������ͼ���ϵĶ��㣬����CD��CF����CD��CFΪ�ڱ���ƽ���ı���CDEF����ƽ���ı���CDEF�����ΪS.
����S�����ֵ��
���ڵ�F���˶������У�����E���ڸö��κ���ͼ����ʱ����ֱ��д����ʱS��ֵ.
���𰸡���1��![]() ��
��![]() ����2����50��
����2����50��![]()
��������
��1����A���B���������![]() �õ�����b��c�ķ����飬Ȼ��ⷽ�������b��c���ɵõ������ߵĽ���ʽ��Ȼ����㺯��ֵΪ0ʱ��Ӧ���Ա�����ֵ���ɵõ�C������
�õ�����b��c�ķ����飬Ȼ��ⷽ�������b��c���ɵõ������ߵĽ���ʽ��Ȼ����㺯��ֵΪ0ʱ��Ӧ���Ա�����ֵ���ɵõ�C������
��2��������DF��OF����ͼ����![]() ������S�ı���OCFD
������S�ı���OCFD![]()
![]() �����������������ʽ�õ�S��CDF=
�����������������ʽ�õ�S��CDF=![]() �������ö��κ��������ʵõ���CDF����������ֵ��Ȼ�����ƽ���ı��ε����ʿɵ�S�����ֵ��
�������ö��κ��������ʵõ���CDF����������ֵ��Ȼ�����ƽ���ı��ε����ʿɵ�S�����ֵ��
�������ı���CDEFΪƽ���ı��Σ���CD��EF��CD=EF������C���D�������������жϵ�C����ƽ��8����λ��������ƽ��4����λ�õ���D�����F����ƽ��8����λ��������ƽ��4����λ�õ���E����![]() ��Ȼ���
��Ȼ���![]() ���������߽���ʽ�õ�����t�ķ��̣��ٽⷽ�����t������CDF��������Ӷ��õ�S��ֵ��
���������߽���ʽ�õ�����t�ķ��̣��ٽⷽ�����t������CDF��������Ӷ��õ�S��ֵ��
�⣺��1����![]() ��
��![]() ����
����![]() �ã�
�ã�
![]() ��
��
���![]()
���������ߵĽ���ʽΪ![]()
��![]() ʱ��
ʱ��![]() �����
�����![]() ��
��![]()
����![]() ������Ϊ
������Ϊ![]()
��2��������![]() ����ͼ����
����ͼ����![]()
��![]()
��![]()
![]()
![]()
��![]() ʱ��
ʱ��![]() ����������ֵ�����ֵΪ25
����������ֵ�����ֵΪ25
���ı���![]() Ϊƽ���ı���
Ϊƽ���ı���
��![]() �����ֵΪ50
�����ֵΪ50
�ڡ��ı���![]() Ϊƽ���ı���
Ϊƽ���ı���
��![]() ��
��![]()
�ߵ�![]() ����ƽ��8����λ��������ƽ��4����λ�õ���
����ƽ��8����λ��������ƽ��4����λ�õ���![]()
���![]() ����ƽ��8����λ��������ƽ��4����λ�õ���
����ƽ��8����λ��������ƽ��4����λ�õ���![]() ����
����![]()
��![]() ����������
����������
��![]() �����
�����![]()
��![]() ʱ��
ʱ��![]()
���ʱ![]() ��
��